太阳高度角

VLoG
次浏览
更新时间:2023-07-18
小编整理:
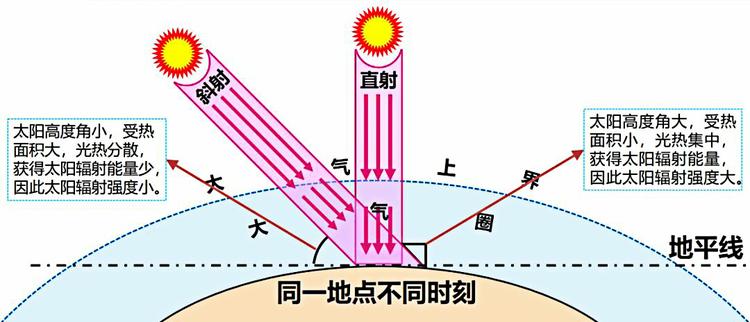
根据题目描述,太阳高度角是指太阳光的入射方向和地平面之间的夹角,专业上讲太阳高度角是指某地太阳光线与通过该地与地心相连的地表切面的夹角。 当太阳高度角为90°时,此时太阳辐射强度最大;当太阳斜射地面时,太阳辐射强度就小。 因此,太阳高度角是影响太阳辐射强度的重要因素。太阳高度角
太阳光入射方向和地平面间的夹角
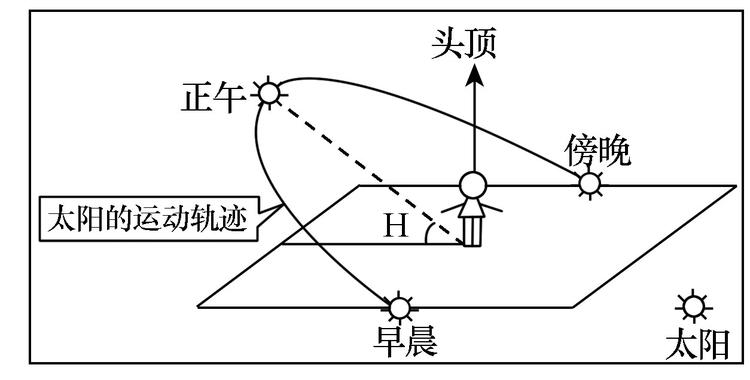
太阳高度角
对于地球上的某个地点,太阳高度角是指太阳光的入射方向和地平面之间的夹角,专业上讲太阳高度角是指某地太阳光线与通过该地与地心相连的地表切面的夹角。太阳高度角简称高度角。当太阳高度角为90°时,此时太阳辐射强度最大;当太阳斜射地面时,太阳辐射强度就小。
基本信息
定义
太阳高度角简称太阳高度(其实是角度)。
太阳高度是决定地球表面获得太阳热能数量的最重要的因素。
一般时间
太阳高度角随着地方时和太阳的赤纬的变化而变化。太阳赤纬(与太阳直射点纬度相等)以δ表示,观测地地理纬度用φ表示(太阳赤纬与地理纬度都是北纬为正,南纬为负),地方时(时角)以t表示,有太阳高度角的计算公式:
sin h= sin φ sin δ+cos φ cosδ cos t
正午时间
日升日落,同一地点一天内太阳高度角是不断变化的。时角是以正午12点为0度开始算,每一小时为15度。即14点和10点分别为30度和-30度。日出日落时角度都为0,正午时太阳高度角最大(90°),时角为0,以上的公式可以简化为:

sin h=sin φ sin δ+cos φ cos δ
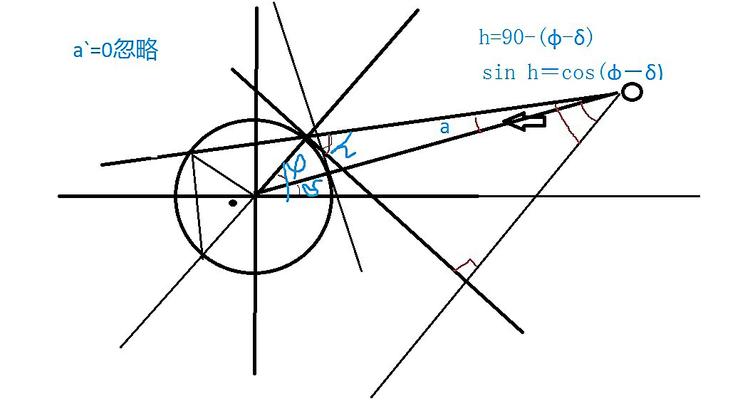
sin h=cos(φ-δ)
因此,
对于太阳位于天顶以北的地区而言,h=90°-(φ-δ);
对于太阳位于天顶以南的地区而言,h=90°-(δ-φ);
二者合并,因为无论是(φ-δ)还是(δ-φ),都是为了求当地纬度与太阳直射纬度之差,不会是负的,因此都等于它的绝对值,所以正午太阳高度角计算公式:
h=90°-|φ-δ|
具体计算:
对于(0°,120°E)这点来说,它离太阳直射点的纬度距离是0°,它的太阳高度角就是90°。
另外一个观测点,(1°N,120°E)与太阳直射点的纬度差为1°
此时,这一点的太阳高度角为89°(根据上面的公式h=90°-|φ-δ|)。
(1°S,120°E)与太阳直射点的纬度差也是1°。
因此,当地的太阳高度角也是89°!
同一时刻,下列各观测点,报告的太阳高度角度数如下:
南北纬2°(与太阳直射点相距2°):88°(=90°-2°)
南北纬3°(与太阳直射点相距3°):87°(=90°-3°)
南北纬30°(与太阳直射点相距30°):60°(=90°-30°)
南北纬80°(与太阳直射点相距80°):10°(=90°-80°)
南北纬90°(与太阳直射点相距90°):0°(=90°-90°)
赤纬算法
上述式子中都涉及太阳赤纬,太阳赤纬的算法如下:
由于太阳赤纬角在周年运动中任何时刻的具体值都是严格已知的,所以它(ED)也可
以用与式(1)相类似的表达式表述,即:
ED=0.3723+23.2567sinθ+0.1149sin2θ-0.1712sin3θ-0.758cosθ+0.3656cos
2θ+0.0201cos3θ(5)
式中θ称日角,即 θ=2πt/365.2422(2)
这里t又由两部分组成,即 t=N-N0 (3)
N0=79.6764+0.2422×(年份-1985)-INT〔(年份-1985)/4〕
(式中INT表示取整数部分,例如INT(3.25)=3)
意义
在晨昏线上的各地太阳高度为0 °,表示正经历昼夜更替;
在夜半球上的各地太阳高度小于0°,表示黑夜。
变化规律
例如:太阳直射20°N,这天全球正午太阳高度角就从20°N向南北两侧逐渐递减,19°N的正午太阳高度角就等于89°。
2、季节变化规律:太阳直射点移来时渐增,移去时渐减(太阳直射点相对某地所在纬线而言)。例如:对于31°N的地区,在12月22日(冬至日)至6月22日(夏至日)这段时间,正午太阳高度角渐增,6月22日(夏至日)至12月22日(冬至日)这段时间,正午太阳高度角渐减。
小结:
1、整个南或北半球,正午太阳高度角能同时达全年最小值(该半球的冬至日),但不能同时达全年最大值;
3、南北回归线上一年一次最大值(该半球的夏至日)和最小值(该半球的冬至日);南北回归线之间的地区一年两次最大值(太阳直射时)、一次最小值(该半球的冬至日),但赤道一年各两次;
4、回归线以外的地区,一年各一次最大值(该半球的夏至日)和最小值(该半球的冬至日)。
发展历程
2015年9月11日开始的全国大学生数学建模竞赛中,其中本科组A题太阳影子定位涉及到了此概念。
2016年5月18日开始的东南大学本科生数学建模竞赛中,其中B题的太阳影子定位涉及到了此概念。
2016年8月18日开始的青岛科技大学数学建模培训中,其中第五题的太阳影子定位涉及到了此概念。


