热力学第二定律(定理定律)

VLoG
次浏览
更新时间:2023-05-17
热力学第二定律
定理定律
定律表述
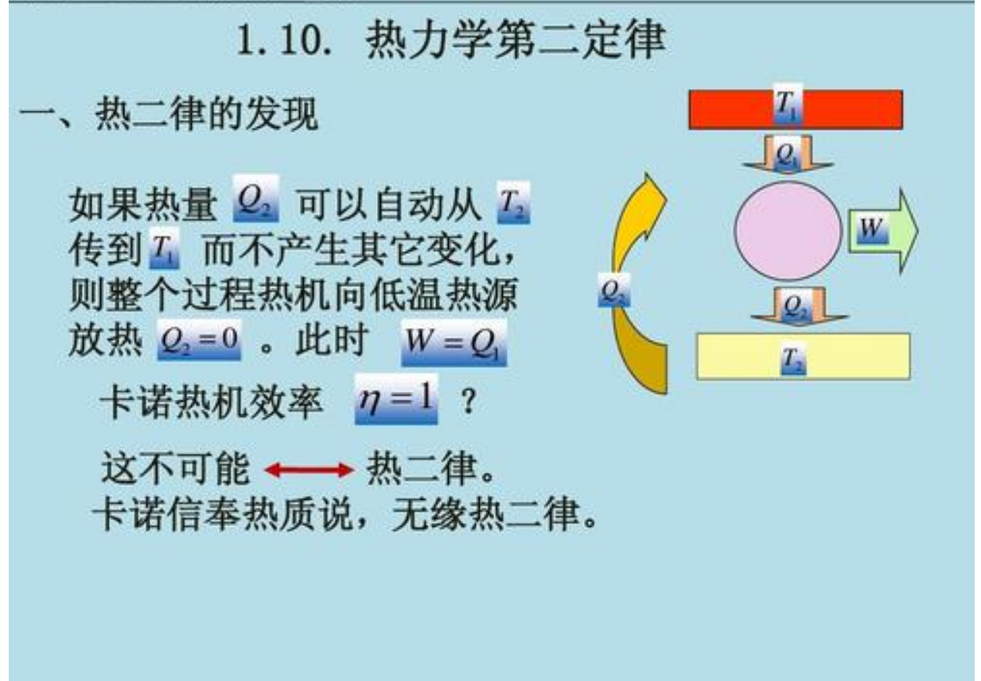
1824年,法国工程师萨迪·卡诺提出了卡诺定理。德国人克劳修斯(Rudolph Clausius)和英国人开尔文(Lord Kelvin)在热力学第一定律建立以后重新审查了卡诺定理,意识到卡诺定理必须依据一个新的定理,即热力学第二定律。他们分别于1850年和1851年提出了克劳修斯表述和开尔文表述。这两种表述在理念上是等价的。
用符号表示,就是dS≥0。
克劳修斯表述
不可能把热量从低温物体传向高温物体而不引起其它变化。
英国物理学家开尔文(原名汤姆逊)在研究卡诺和焦耳的工作时,发现了某种不和谐:按照能量守恒定律,热和功应该是等价的,可是按照卡诺的理论,热和功并不是完全相同的,因为功可以完全变成热而不需要任何条件,而热产生功却必须伴随有热向冷的耗散。他在1849年的一篇论文中说:“热的理论需要进行认真改革,必须寻找新的实验事实。”同时代的克劳修斯也认真研究了这些问题,他敏锐地看到不和谐存在于卡诺理论的内部。他指出卡诺理论中关于热产生功必须伴随着热向冷的传递的结论是正确的,而热的量(即热质)不发生变化则是不对的。克劳修斯在1850年发表的论文中提出,在热的理论中,除了能量守恒定律以外,还必须补充另外一条基本定律:“没有某种动力的消耗或其他变化,不可能使热从低温转移到高温。”这条定律后来被称作热力学第二定律。
开尔文表述
不可能制成一种循环动作的热机,从单一热源取热,使之完全变为功而不引起其它变化。
这是从能量消耗的角度说的。开尔文表述还可以表述成:第二类永动机不可能实现。
开尔文的表述更直接指出了第二类永动机的不可能性。所谓第二类永动机,是指某些人提出的例如制造一种从海水吸取热量,利用这些热量做功的机器。这种想法,并不违背能量守恒定律,因为它消耗海水的内能。大海是如此广阔,整个海水的温度只要降低一点点,释放出的热量就是天文数字,对于人类来说,海水是取之不尽、用之不竭的能量源泉,因此这类设想中的机器被称为第二类永动机。而从海水吸收热量做功,就是从单一热源吸取热量使之完全变成有用功并且不产生其他影响,开尔文的说法指出了这是不可能实现的,也就是第二类永动机是不可能实现的。
熵增加原理
熵增加原理是热力学第二定律的又一种表述,它比开尔文、克劳修斯表述更为概括地指出了不可逆过程的进行方向;同时,更深刻地指出了热力学第二定律是大量分子无规则运动所具有的统计规律,因此只适用于大量分子构成的系统,不适用于单个分子或少量分子构成的系统。
定律的其他表述
“不可存在一个机器,在循环动作中把以重物升高而同时使一热库冷却。”
以及较为近期的黑首保劳-肯南表述(Hatsopoulos-Keenan statement):
“对于一个有给定能量,物质组成,参数的系统,存在这样一个稳定的平衡态:其他状态总可以通过可逆过程达到之。”
可以论证,这些表述与克劳修斯表述以及开尔文表述是等价的。
热力学第二定律说明:热量可以自发地从较热的物体传递到较冷的物体,但不可能自发地从较冷的物体传递到较热的物体(克劳修斯表述);也可表述为:两物体相互摩擦的结果使功转变为热,但却不可能将这摩擦热重新转变为功而不产生其他影响。对于扩散、渗透、混合、燃烧、电热和磁滞等热力过程,虽然其逆过程仍符合热力学第一定律,但却不能自发地发生。热力学第一定律未解决能量转换过程中的方向、条件和限度问题,这恰恰是由热力学第二定律所规定的。
定律解释
形成
热力学第二定律是热力学的基本定律之一,是指热永远都只能由热处转到冷处(在自然状态下)。它是关于在有限空间和时间内,一切和热运动有关的物理、化学过程具有不可逆性的经验总结。
在的讲法中指出,自然界中任何形式的能都会很容易地变成热,而反过来热却不能在不产生其他影响的条件下完全变成其他形式的能,从而说明了这种转变在自然条件下也是不可逆的。热机能连续不断地将热变为机械功,一定伴随有热量的损失。第二定律和第一定律不同,第一定律否定了创造能量和消灭能量的可能性,第二定律阐明了过程进行的方向性,否定了以特殊方式利用能量的可能性。
人们曾设想制造一种能从单一热源取热,使之完全变为有用功而不产生其他影响的机器,这种空想出来的热机叫第二类永动机。它并不违反热力学第一定律,但却违反热力学第二定律。有人曾计算过,地球表面有10亿立方千米的海水,以海水作单一热源,若把海水的温度哪怕只降低0。25度,放出热量,将能变成一千万亿度的电能足够全世界使用一千年。但只用海洋做为单一热源的热机是违反上述第二种讲法的,因此要想制造出热效率为百分之百的热机是绝对不可能的。
从分子运动论的观点看,作功是大量分子的有规则运动,而热运动则是大量分子的无规则运动。显然无规则运动要变为有规则运动的几率极小,而有规则的运动变成无规则运动的几率大。一个不受外界影响的孤立系统,其内部自发的过程总是由几率小的状态向几率大的状态进行,从此可见热是不可能自发地变成功的。
热力学第二定律只能适用于由很大数目分子所构成的系统及有限范围内的宏观过程。而不适用于少量的微观体系,也不能把它推广到无限的宇宙。
根据热力学第一定律,确定了态函数——内能和焓;
根据热力学第二定律,也可以确定一个新的态函数——熵。可以用熵来对第二定律作定量的表述。
过程
第二定律指出在自然界中任何的过程都不可能自动地复原,要使系统从终态回到初态必需借助外界的作用,由此可见,热力学系统所进行的不可逆过程的初态和终态之间有着重大的差异,这种差异决定了过程的方向,人们就用态函数熵来描述这个差异,从理论上可以进一步证明:
可逆绝热过程Sf=Si,
不可逆绝热过程Sf>Si,
式中Sf和Si分别为系统的最终和最初的熵。
也就是说,在孤立系统内对可逆过程,系统的熵总保持不变;对不可逆过程,系统的熵总是增加的。这个规律叫做熵增加原理。这也是热力学第二定律的又一种表述。熵的增加表示系统从几率小的状态向几率大的状态演变,也就是从比较有规则、有秩序的状态向更无规则,更无秩序的状态演变。熵体现了系统的统计性质。
条件
第二定律在有限的宏观系统中也要保证如下条件:
1.该系统是线性的;
2.该系统全部是各向同性的。
定律质疑
麦克斯韦妖
麦克斯韦妖是詹姆斯·麦克斯韦假想存在的一理想模型。麦克斯韦设想了一个容器被分为装有相同温度的同种气体的两部分A、B。麦克斯韦妖看守两部分间“暗门”,可以观察分子运动速度,并使分子运动较快的分子向确定的一部分流动,而较慢的分子向另一部分流动。经过充分长的时间,两部分分子运动的平均速度即温度(参考统计力学中对于温度的微观解释)产生差值并越来越大。经过运算可以得到这一过程是熵减过程,而麦克斯韦妖的存在使这一过程成为自发过程,这是明显有悖于热力学第二定律的。
对其最为有名的回应之一是由列奥·西拉德于1929年提出。西拉德指出如果麦克斯韦妖真正存在,那么它观察分子速度及获取信息的过程必然产生额外的能量消耗,产生熵。
洛施密特悖论
针对这一悖论,玻尔兹曼提出:熵增过程确实并非一个单调过程,但对于一个宏观系统,熵增出现要比熵减出现的概率要大得多;即使达到热平衡,熵也会围绕着其最大值出现一定的涨落,且幅度越大的涨落出现概率越小。现在已有的一些实验结果,与玻尔兹曼的叙述基本相符。
热力学第二定律是建立在对实验结果的观测和总结的基础上的定律。虽然在过去的一百多年间未发现与第二定律相悖的实验现象,但始终无法从理论上严谨地证明第二定律的正确性。自1993年以来,Denis J.Evans等学者在理论上对热力学第二定律产生了质疑,从统计热力学的角度发表了一些关于“熵的涨落“的理论,比如其中比较重要的FT理论。而后G.M.Wang等人于2002在Physical Review Letters上发表了题为《小系统短时间内有悖热力学第二定律的实验证明》。从实验观测的角度证明了在一定条件下热,孤立系统的自发熵减反应是有可能发生的。
吉布斯悖论
玻尔兹曼关系给出了一个并不外延的熵的表示方法。这导致产生了一个明显有悖于热力学第二定律的结论,吉布斯悖论——其允许一个封闭系统的熵减少。在通常的解释中,都会引用量子力学中粒子的不可区分性去说明系统中粒子本身性质并不影响系统的熵来避免产生这一悖论。然而现在有越来越多论文采用如是观点:熵阐释的改变恰恰可以忽略由于分子本身排列方式改变所带来的影响。而现有的Sackur-Tetrode方程对于理想气体的熵的解释是外延的。
热寂论

热寂
在十九世纪,对于热寂说有两个较为有影响的驳斥,一个是由玻尔兹曼提出的“涨落说”(1872),另一个是恩格斯利用运动不灭在《自然辩证法》中进行的驳斥(1876)。现今对于宇宙的理解(1.宇宙在膨胀;2.宇宙,作为自引力系统,是具有负热容的不稳定系统)指出宇宙是不稳定的热力学系统,并不像静态宇宙模型所设想的那样具有平衡态,因而其熵亦无最大值,即热寂并不存在。
参考资料
[1]
北京师范大学无机化学教研室等编 . 无机化学.上册(第4版) : 北京:高等教育出版社 ,2002
相关视频
全部
2.8万次播放04:01
为什么你斗地主大多数摸到的不是两王三A四个2!热力学定理告诉你


