高斯定理(应用于数学等学科的理论)

VLoG
次浏览
更新时间:2023-05-20
高斯定理
应用于数学等学科的理论
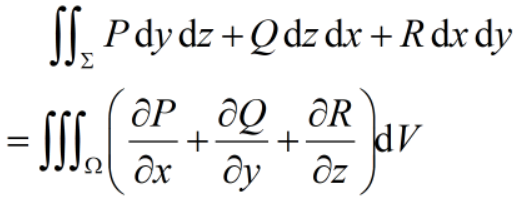
对于一个矢量场V,其散度的体积分等于V在此体积表面上的法向分量的面积分,上述定理被成为高斯定理(英文:Gauss's law),又称为散度定理(Divergence theorem)。
基本信息
中文名
高斯定理
英文名
Gauss's law,Divergence theorem
提出时间
1813年
相关人物
奥斯特洛格拉特斯基、高斯
高斯定理把矢量场通过曲面的流动(即通量)与曲面内部的向量场的表现联系了起来,将复杂的曲面积分计算转化为较为简单的三重积分运算,在电磁学等领域中也具有运用。
基本概念
若某封闭区域空间






证明
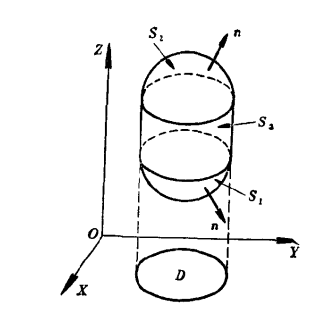
首先假设







当

同理可证:


将上述三个等式相加,即得到高斯定理。
历史
1826年,苏联数学家奥斯特洛格拉特斯基(Mikhail Ostrogradsky)首先撰文发表了散度定理。由于德国数学家约翰·卡尔·弗里德里希·高斯(Karl Friedrich Gauss)在1813年他的著作中已经研究了这一定理,只是未及时发表,因此散度定理也称为高斯定理。
其他形式
第一类曲面积分形式
由两类曲面之间的联系立即可以给出高斯公式的第一类曲面积分形式:

矢量形式
高斯定理也可以从场论的观点进行阐释。场论是运用数学理论研究某些物理量在空间中的分布状态,如果该物理量为标量,如温度等,则对应的场如温度场等称为标量场。如果该物理量为矢量,如速度等,则对应的场如速度场等称为矢量场。在空间直角坐标系中,一个矢量场


高斯定理的公式左端可以表示为:

则











对于上述的矢量场


与通量类似,散度也是矢量场的一个重要物理量,表示在场中的某一点处通量对体积的变化率。当散度不为0时,称该区域内是有源的,当散度恒为0时,则该区域是无源。
在引入通量和散度的定义后,高斯定理可以表示如下的矢量形式:

从场的观点来看,高斯定理描述了矢量场在某封闭区域中的通量和散度之间的关系,即矢量场



微分形式
若规定一个作用于




由散度的定义式可得:

得到结果如下:

上式也称为高斯定理的微分形式。
相关推论
- 若某封闭区域空间




(1)



(2)沿任何一个闭合曲面


(3)以下曲面积分与




电磁场中的高斯定理
静电场的高斯定理
静电场中的高斯定理给出了静电场中通过任一闭合曲面的电通量与该闭合曲面内所包围的电荷之间的量值关系,是静电场的一条基本定理。具体来说,在真空中的静电场中,任一闭合面






静电场的高斯定理同样适用于恒定电场中。
磁场的高斯定理
在磁场中,对于任意一个闭合曲面,由于磁感线是闭合曲线,即磁感线进入和传出闭合曲面的数量总是相等的,因此通过任何闭合曲面的总磁通量必为零,称为磁场的高斯定理,也称磁通连续定理,它表明磁场是无源场,用公式表示如下:





