晶格常数(晶格中晶胞的物理尺寸)

VLoG
次浏览
更新时间:2023-05-20
晶格常数
晶格中晶胞的物理尺寸
基本信息
| 中文名 | 晶格常数 |
| 别名 | lattice constant |
| 外文名 | 点阵常数 |
| 拼音 | jīng gé cháng shù |
详细信息
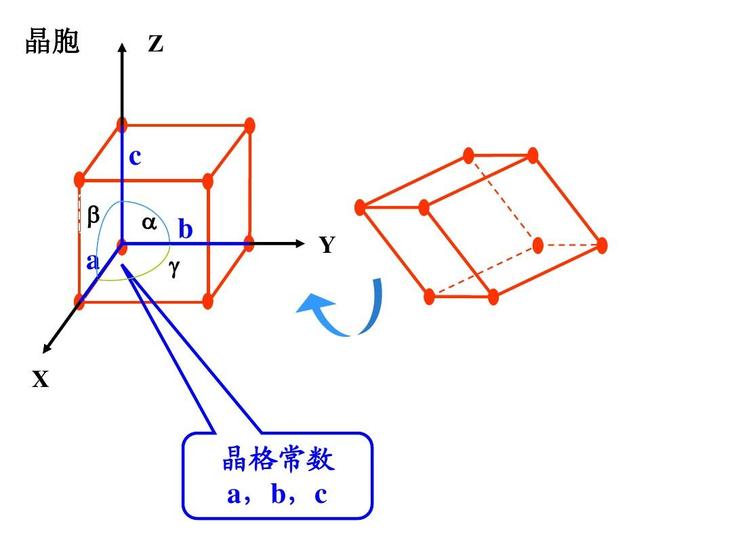
在材料科学研究中,为了便于分析晶体中粒子排列,可以从晶体的点阵中取出一个具有代表性的基本单元(通常是最小的平行六面体)作为点阵的组成单元,称为晶胞,晶胞不一定是最小的重复单元,其一般是原胞(一般认为原胞是组成晶体的最小单元)体积的整数倍。
三维空间中的晶格一般有3个晶格常数,分别用a,b和c来表示。但在立方晶体结构这一特殊情形下,这3个常数都相等,故仅用a来表示。类似的情形还有六方晶系结构,其中a和b这两个常数相等,因此我们只用a和c。一族晶格常数也可合称为晶格参数(latticeparameter)。但实际上,完整的晶格参数应当由3个晶格常数和3个夹角来描述。
例如,对于常见的金刚石,其晶格常数为a=3.57Å(300K)。这里的晶胞是等边结构,但是仅从晶格常数并不能推知金刚石的实际结构。此外,在实际应用中,通常给出的平均晶格常数。在晶体的表面,晶格常数是受表面重建,其平均值的偏差的结果。这种偏差是特别重要的纳米晶体由于表面纳米晶核比大。随着晶格常数的长度尺寸,其SI单位是米。晶格常数通常在几埃的数量级(即零点几纳米)。晶格常数可以使用的技术,如X射线衍射和原子力显微镜测定。
在外延生长,晶格常数是衡量不同材料之间的结构相容性。晶格常数匹配的其他材料的薄层的材料的成长很重要;当常数不同,菌株引入层,防止厚层外延生长无缺陷。
晶格匹配
格的分级
问题
计算未知物质的晶格常数?
对于立方体结构,在粉末样品中加入少量衍射本身高的物质,如Si粉,精确地测量与某个硅峰较接近的一个样品峰,计算出两个峰的衍射角,再查一下PDF卡片上硅峰的正确衍射角,加上测量值与标准值之差,就得到精确的无仪器误差的衍射峰,再按晶体学计算公式就可以计算出来点阵常数了。非立方结构就麻烦多了。基本上无法用这种方法来计算。而且,这种计算还是含有误差的,因为只有当衍射角等于90时才无系统误差。如果用软件,如JADE,则要用完全相同的实验条件来测量一个纯硅样和样品的衍射谱全谱,按软件的方法去掉仪器误差再用全谱拟合的办法来得到精修的结果。后一种方法可以分别计算多相样品中各不同的相的晶胞参数。由于测量的是全谱,对复杂结构的相也可以计算。但精度明显不如单相的结果。


