反函数(适用于解析几何学等的函数)

VLoG
次浏览
更新时间:2023-05-22
反函数
适用于解析几何学等的函数
定义
设函数 的定义域是D,值域是f(D)。如果对于值域f(D)中的每一个y,在D中有且只有一个x使得
的定义域是D,值域是f(D)。如果对于值域f(D)中的每一个y,在D中有且只有一个x使得 ,则按此对应法则得到了一个定义在f(D)上的函数,并把该函数称为函数
,则按此对应法则得到了一个定义在f(D)上的函数,并把该函数称为函数 的反函数,记为
的反函数,记为 由该定义可以很快得出函数f的定义域D和值域f(D)恰好就是反函数
由该定义可以很快得出函数f的定义域D和值域f(D)恰好就是反函数 的值域和定义域,并且
的值域和定义域,并且 的反函数就是f,也就是说,函数f和
的反函数就是f,也就是说,函数f和 互为反函数,即:
互为反函数,即:









例如,函数 的反函数是
的反函数是 。
。


相对于反函数 来说,原来的函数
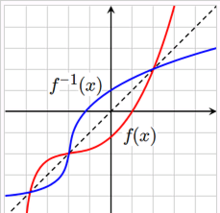
来说,原来的函数 称为直接函数。反函数和直接函数的图像关于直线
称为直接函数。反函数和直接函数的图像关于直线 对称。这是因为,如果设(a,b)是
对称。这是因为,如果设(a,b)是 的图像上任意一点,即
的图像上任意一点,即 。根据反函数的定义,有
。根据反函数的定义,有 ,即点(b,a)在反函数
,即点(b,a)在反函数 的图像上。而点(a,b)和(b,a)关于直线
的图像上。而点(a,b)和(b,a)关于直线 对称,由(a,b)的任意性可知f和
对称,由(a,b)的任意性可知f和 关于
关于 对称。
对称。










于是我们可以知道,如果两个函数的图像关于 对称,那么这两个函数互为反函数。这也可以看做是反函数的一个几何定义。
对称,那么这两个函数互为反函数。这也可以看做是反函数的一个几何定义。

若一函数有反函数,此函数便称为可逆的(invertible)。
存在性
反函数存在定理
定理:严格单调函数必定有严格单调的反函数,并且二者单调性相同。
在证明这个定理之前先介绍函数的严格单调性。
设 的定义域为D,值域为f(D)。如果对D中任意两点
的定义域为D,值域为f(D)。如果对D中任意两点 和
和 ,当
,当  时,有
时,有  ,则称
,则称 在D上严格单调递增;当
在D上严格单调递增;当 时,有
时,有 ,则称
,则称 在D上严格单调递减。
在D上严格单调递减。









证明:设f在D上严格单增,对任一 ,有
,有


而由于f的严格单增性,对D中任一 ;任一
;任一 总之能使
总之能使 的x只有一个,根据反函数的定义,f存在反函数
的x只有一个,根据反函数的定义,f存在反函数 。
。




任取f(D)中的两点 和
和 ,设
,设 <
< 。而因为f存在反函数
。而因为f存在反函数 ,所以有
,所以有  ,
,  ,且
,且  。
。








若此时  ,根据f的严格单增性,有
,根据f的严格单增性,有 ,这和我们假设的
,这和我们假设的 矛盾。
矛盾。



因此  ,即当
,即当 时,有
时,有 。这就证明了反函数f也是严格单增的。
。这就证明了反函数f也是严格单增的。



如果f在D上严格单减,证明类似。
性质
反函数的符号
反函数的反函数
为了好看以及对比,我有时会把f(x)写成f对比,我把我想各位应该很好理解,反函数的反函数当然就是原函数,写成数学语言就是 。看看,这是不是有点像指数的运算法则:
。看看,这是不是有点像指数的运算法则: 呢?
呢?


反函数的导函数
如果函数 在区间Iy内单调、可导且
在区间Iy内单调、可导且 不等于零,则它的反函数
不等于零,则它的反函数 在区间
在区间 内也可导,且
内也可导,且 或
或 。
。






用自然语言来说就是,反函数的导数,等于直接函数导数的倒数。这话有点绕,不过应该能读懂,这个似乎就进一步揭示了反函数符号的意义。
反函数的复合函数
数字的基本运算就是加减乘除,而函数也有运算,虽然也有加减乘除,但是属于函数自己的,就是复合与反函数。我们知道在实数里,x与 的乘积等于1,在函数的复合运算里,也有类似的性质,函数f和g的复合记为
的乘积等于1,在函数的复合运算里,也有类似的性质,函数f和g的复合记为 ,那么下面的性质成立:
,那么下面的性质成立: 。
。



这第一个式子已经说明很多问题。实际上,这些都是属于高等代数的内容,在每一个封闭的系统里,都有一个“单位1”,都有自己的运算法则,函数里的就是 ,实数里的就是数字1等等。要深刻理解这些,也只有大家接触群论以后才会深入理解。这里也只是做点皮毛而已。我将在后面另起一文,介绍函数的“幂”的概念,就如同数的幂一样。
,实数里的就是数字1等等。要深刻理解这些,也只有大家接触群论以后才会深入理解。这里也只是做点皮毛而已。我将在后面另起一文,介绍函数的“幂”的概念,就如同数的幂一样。

说明
(1)在函数 中,y是自变量,x是函数,但习惯上,我们一般用x表示自变量,用y 表示函数,为此我们常常对调函数
中,y是自变量,x是函数,但习惯上,我们一般用x表示自变量,用y 表示函数,为此我们常常对调函数 中的字母x,y,把它改写成
中的字母x,y,把它改写成 ,今后凡无特别说明,函数
,今后凡无特别说明,函数 的反函数都采用这种经过改写的形式。
的反函数都采用这种经过改写的形式。




⑵反函数也是函数,因为它符合函数的定义. 从反函数的定义可知,对于任意一个函数 来说,不一定有反函数,若函数
来说,不一定有反函数,若函数 有反函数
有反函数 ,那么函数
,那么函数 的反函数就是
的反函数就是 ,这就是说,函数
,这就是说,函数 与
与 互为反函数。
互为反函数。







⑷ 从映射的定义可知,函数 是定义域A到值域C的映射,而它的反函数
是定义域A到值域C的映射,而它的反函数 是集合C到集合A的映射,因此,函数
是集合C到集合A的映射,因此,函数 的定义域正好是它的反函数
的定义域正好是它的反函数 的值域;函数
的值域;函数 的值域正好是它的反函数
的值域正好是它的反函数 的定义域(如下表):
的定义域(如下表):






函数: ;
;

反函数: ;
;

定义域: A,C;
值域: C,A;
⑷上述定义用“逆”映射概念可叙述为:
若确定函数 的映射f是函数的定义域到值域上的“一一映射”,那么由f的“逆”映射
的映射f是函数的定义域到值域上的“一一映射”,那么由f的“逆”映射 所确定的函数
所确定的函数 (就叫做函数y=f(x)的反函数. 反函数
(就叫做函数y=f(x)的反函数. 反函数 的定义域、值域分别对应原函数
的定义域、值域分别对应原函数 的值域、定义域.。开始的两个例子:
的值域、定义域.。开始的两个例子: 则它的反函数就可以写为
则它的反函数就可以写为 ,同样
,同样 记为
记为 ,则它的反函数为:
,则它的反函数为: .
.










有时是反函数需要进行分类讨论,如: ,需将x进行分类讨论:在x大于0时的情况,x小于0的情况,多是要注意的。
,需将x进行分类讨论:在x大于0时的情况,x小于0的情况,多是要注意的。