质能方程（阿尔伯特·爱因斯坦提出的方程）
VLoG
次浏览
更新时间：2023-05-22
公式简介
表达形式
表达形式1：
表达形式2：
为随运动速度增大而增大了的质量。
为物体运动时的能量，即物体的静止能量和动能之和。
表达形式3：
上式中的Δm通常为物体静止质量的变化，即质量亏损。ΔE为物体静止能量的变化。实际上这种表达形式是表达形式1的微分形式。这种表达形式最常用，也是学生最容易产生误解的表达形式。
推导1
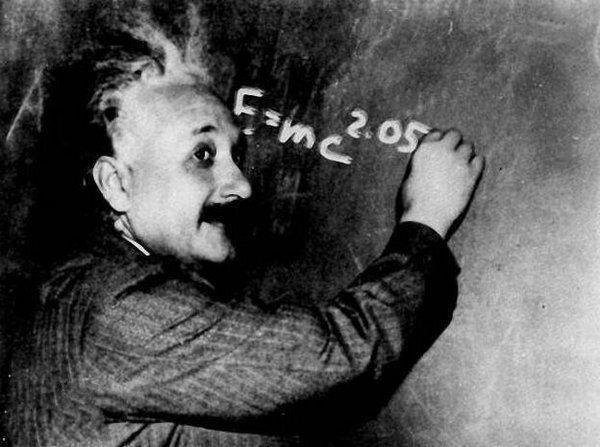
爱因斯坦书写质能方程
而以上这个变换恰恰与狭义相对论的假设相矛盾。
事实上，在爱因斯坦提出狭义相对论之前，人们就观察到许多与常识不符的现象。物理学家洛伦兹为了修正将要倾倒的经典物理学大厦，提出了洛伦兹变换，但他并不能解释这种现象为何发生，只是根据当时的观察事实写出的经验公式——洛伦兹变换——而它却可以通过相对论的纯理论推导出来。
然后根据这个公式又可以推导出质速关系，也就是时间会随速度增加而变慢，质量变大，长度减小。
一个物体的实际质量为其静止质量与其通过运动多出来的质量之和。
当外力作用在静止质量为
的自由质点上时，质点每经历位移
，其动能的增量是
,如果外力与位移同方向，则上式成为
，
考虑到
，有上两式相除，即得质点的速度表达式为
，
亦即
，
注意到等式右边为0，即上式可化为
代入上式得
。
上式说明，当质点的速度v增大时，其质量
和动能
都在增加，质量的增量dm和动能的增量 之间始终保持 所示的量值上的正比关系。
当
时，质量
，动能
，
据此，将上式积分，即得
。
推导：
首先是狭义相对论得到
洛伦兹因子
所以，运动物体的质量
推导2
根据 公式
，运动时物体质量增大，同时运动时将会有动能，质量与动能均随速度增大而增大。
根据
，得
，因为
，所以
，由 易得
。
将该式对m 和v 进行微分，得
，代入 得，对其积分，
。
这就是相对论下的动能公式。当速度为0，
，动能为0。
为物体静止时的能量，而 
，因此总能量
。
影响
这个等式源于阿尔伯特·爱因斯坦对于物体惯性和它自身能量关系的研究。研究的著名结论就是物体质量实际上就是它自身能量的量度。为了便于理解此关系的重要性，可以比较一下电磁力和引力。电磁学理论认为，能量包含于与力相关而与电荷无关的场（电场和磁场）中。在万有引力理论中，能量包含于物质本身。因此物质质量能够使时空扭曲，但其它三种基本相互作用（电磁相互作用，强相互作用，弱相互作用）的粒子却不能，这并不是偶然的。
这个方程对于原子弹的发展是关键性的。通过测量不同原子核的质量和那个数量的独立质子和中子的质量和的差，可以得到原子核所包含的结合能的估计值。这不仅显示可能通过轻核的核聚变和重核的核裂变释放这个结合能，也可用于估算会释放的结合能的量。注意质子和中子的质量还在那里，它们也代表了一个能量值。
一个著名的花絮是爱因斯坦最初将方程写为
（用了一个“L"，而不是“E"来表示能量，而E在其它地方也用来表示能量）。
重要的是要注意实际的静质量到能量的转换不大可能是百分之百有效的。一个理论上完美的转化是物质和反物质的湮灭；对于多数情况，有很多带静质量的副产品而不是能量，因而只有少量的静质量真正被转换。在该方程中，质量就是能量，但是为了简明起见，转换这个词常常被用于代替质能等价关系，实际上通常所指的一般是静质量和能量的转换。
相关
亏损守恒
当一组粒子构成复合物体时，由于各粒子之间有相互作用能以及有相对运动的动能，因而，当物体整体静止时，它的总能量一般不等于所有粒子的静止能量之和，即
，其中 
为第i个粒子的静止质量。
两者之差称为物体的结合能：
与此对应，物体的静止质量
亦不等于组成它的各粒子的静止质量之和，两者之差称为质量亏损：
质量亏损与结合能之间有关系：
由于在中学物理教材中，对此式的解释较浅，因此，有些学生就误认为核反应过程中，质量不再守恒，且少掉的质量转化为能量了。
守恒定律
在相对论里，质能公式 
描述了质量与能量存在固定关系。在经典力学中，质量和能量之间是相互独立、没有关系的，但在相对论力学中，能量和质量只不过是物体力学性质的两个不同方面而已。这样，在相对论中质量这一概念的外延就被大大地扩展了。爱因斯坦指出：“如果有一物体以辐射形式放出能量ΔE，那么它的质量就要减少
.至于物体所失去的能量是否恰好变成辐射能，在这里显然是无关紧要的，于是我们被引到了这样一个更加普遍的结论上来。物体的质量是它所含能量的量度，”他还指出，“这个结果有着特殊的理论重要性，因为在这个结果中，物体系的惯性质量和能量以同一种东西的姿态出现……我们无论如何也不可能明确地区分体系的‘真实’质量和‘表现’质量。把任何惯性质量理解为能量的一种储藏，看来要自然得多。”这样，原来在经典力学中彼此独立的质量守恒和能量守恒定律结合起来，成了统一的“质能守恒定律”，它充分反映了物质和运动的统一性。质能方程说明，质量和能量是不可分割而联系着的。一方面，任何物质系统既可用质量m来标志它的数量，也可用能量E来标志它的数量；另一方面，一个系统的能量减少时，其质量也相应减少，另一个系统接受而增加了能量时，其质量也相应地增加。
质能方程——著名的公式，人们把这个方程叫做爱因斯坦质能方程。
附加项：揭示质能方程的隐藏秘密
引言
质能方程:
能量等於质量及光的平方。实实在在让人模不著头脑，能量与质量之比，关光什麼事???
这问题，使绝大部分对研究物理的科学家们头痛万分，在公布的最初甚至到现在有些科学家们仍然认为这方程是错误的。但无数实验确确实实的数据显示，质能方程准确无误。但其原因，依旧使人迷茫。
对科研人来说，是个''真实而又正确的谜''。
1 质能场方程
1.1质能方程的隐藏意义
爱因斯坦的推导，上面公式的实验结果，这里就不再贴了，反正很多种推导教科书也有。
这里我们来看看这方程的隐藏意义。
先来看看光的平方是什麼:
即质能方程可改成:
只是稍微的改变一下这公式的表达式，我们就可看见一个新奇的现象，
这样，直接以这公式，我们就可以引述一个现象:
质量，是基於
这结构上存在多少E能量而形成的。
所以，质量，是一个由这结构而来的能量场。
所以
应该写成下面的表达式:
----我们称这表达式为''质能场方程''。
所以, 质量, 是一个由空间形成的能量场。
出售
2021年5月，世界著名物理学家爱因斯坦亲手书写的、带有他著名公式的信函，在波士顿RR Auction拍卖行，以超过120万美元的价格售出。
参考资料
[1]
超120万美元！写有著名公式的爱因斯坦亲笔信拍卖售出 · 央视网[引用日期2021-05-23]
