等周问题(1901年赫尔维茨提出的概念)-尚可名片

等周问题（1901年赫尔维茨提出的概念）

VLoG

次浏览

更新时间：2023-05-22

等周问题

1901年赫尔维茨提出的概念

等周定理，又称等周不等式，是一个几何中的不等式定理，说明了欧几里得平面上的封闭图形的周长以及其面积之间的关系。其中的“等周”指的是周界的长度相等。

基本信息

收起

简介

等周定理说明在周界长度相等的封闭几何形状之中，以圆形的面积最大；另一个说法是面积相等的几何形状之中，以圆形的周界长度最小。它可以以不等式表达：

P若为封闭曲线的周界长，A为曲线所包围的区域面积，

虽然等周定理的结论早已为人所知，但要严格的证明这一点并不容易。首个严谨的数学证明直到19世纪才出现。之后，数学家们陆续给出了不同的证明，其中有不少是非常简单的。等周问题有许多不同的推广，例如在各种曲面而不是平面上的等周问题，以及在高维的空间中给定的“表面”或区域的最大“边界长度”问题等。

在物理中，等周问题和跟所谓的最小作用量原理有关。一个直观的表现就是水珠的形状。在没有外力的情况下（例如失重的太空舱里），水珠的形状是完全对称的球体。这是因为当水珠体积一定时，表面张力会迫使水珠的表面积达到最小值。根据等周定理，最小值是在水珠形状为球状时达到。

详解

等周问题

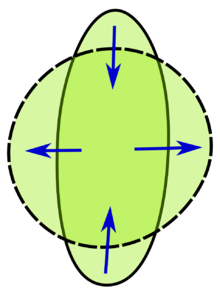
不完全凸的封闭曲线的话，能以“翻折”凹的部分以成为凸的图形，以增加面积，而周长不变

等周问题

一个狭长的图形可以通过“压扁”来变得“更圆”，从而使得面积更大而周长不变。

平面上的等周问题是等周问题最经典的形式，它的出现可以追溯到很早以前。这个问题可以被表述为：在平面上所有周长一定的封闭曲线中，是否有一个围成的面积最大？如果有的话，是什么形状？另一种等价的表述是：当平面上的封闭曲线围成的面积一定时，怎样的曲线周长最小？

虽然圆看似是问题的表面答案，但证明此事实其实不易。首个接近答案的步骤出现在1838年——雅各·史坦纳以几何方法证明若答案存在，答案必然是圆形。不久之后他的证明被其他数学家完善。

其方法包括证明了不完全凸的封闭曲线的话，能以“翻折”凹的部分以成为凸的图形，以增加面积；不完全对称的封闭曲线能以倾斜来取得更多的面积。圆，是完全凸和对称的形状。可是这些并不足以作为等周定理的严格证明。

1901年，赫尔维茨凭傅里叶级数和格林定理给出一个纯解析的证明。

2012年，潘忆思利用不等式给出了一个十分简单初等证明。论文名称《不等式与等周问题》。