判别式（判断方程实根个数的公式）
VLoG
次浏览
更新时间：2023-05-22
判别式
判断方程实根个数的公式
定义
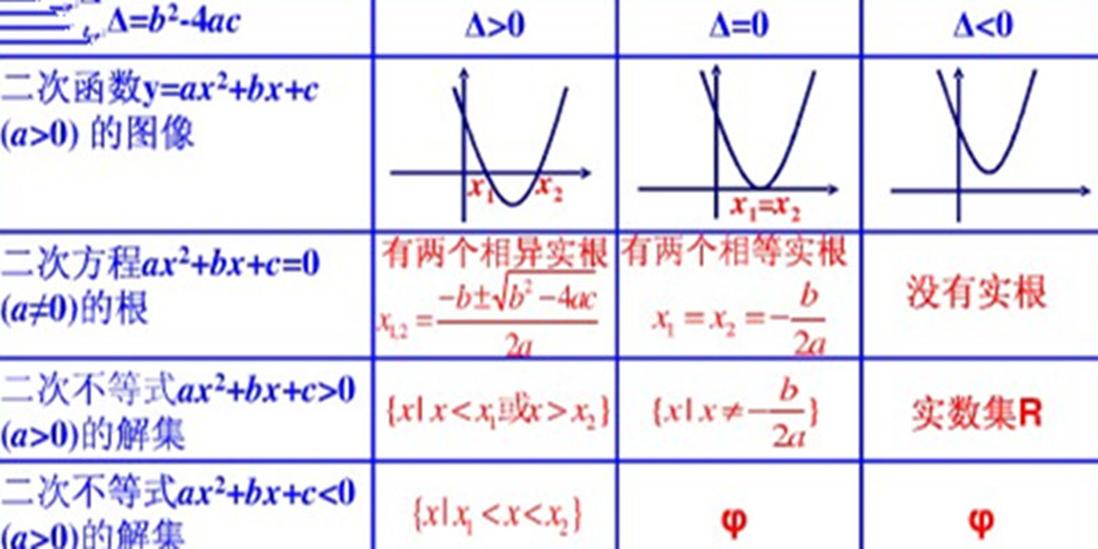
判别式即判定方程实根个数及分布情况的公式。
一元二次方程
任意一个一元二次方程
均可配成
，因为a≠0，由平方根的意义可知，
的符号可决定一元二次方程根的情况．
根的情况
方程系数为实数
在一元二次方程 中
（1）当
时，方程有两个不相等的实数根；
（2）当
时，方程有两个相等的实数根；
（1）和（2）合起来：当
时，方程有实数根．
上面结论反过来也成立，可以具体表示为：
在一元二次方程
（
）中，
①当方程有两个不相等的实数根时，；
②当方程有两个相等的实数根时，；
③当方程没有实数根时，
。
（1）和（2）合起来：当方程有实数根时，．
注意 根的判别式是
，而不是
。
当
≥0时，
，
当
时，
;
方程系数为虚数
在一元二次方程（a、b、c是虚数）中
当
时，此方程有两个相等的复根；
当
时，此方程有两个不等的复根。
应用
它有两种不同层次的类型：
①系数都为数字；
②系数中含有字母；
③系数中的字母人为地给出了一定的条件．
（2）根据一元二次方程根的情况，确定方程中字母的取值范围或字母间关系．
（3）应用判别式证明方程根的情况（有实根、无实根、有两不等实根、有两相等实根）
应用
① 解一元二次方程，判断根的情况。
② 根据方程根的情况，确定待定系数的取值范围。
④ 应用根的判别式判断三角形的形状。
⑤ 判断当字母的值为何值时，二次三项是完全平方式
⑥ 可以判断抛物线与直线有无公共点
联立方程。
⑦ 可以判断抛物线与x轴有几个交点
抛物线
与x轴的交点（1）当
时，即有，要求x的值，需解一元二次方程。可见，抛物线 与x轴的交点的个数是由对应的一元二次方程 的根的情况确定的，而决定一元二次方程 的根的情况的，是它的判别式的符号，因此抛物线与x轴的交点有如下三种情形：
1）当
时，抛物线与x轴有两个交点，若此时一元二次方程 的两根为
，则抛物线与x轴的两个交点坐标为
。
2）当时，抛物线与x轴有唯一交点，此时的交点就是抛物线的顶点，其坐标是（
，0）。
3）当 时，抛物线与x轴没有交点。
⑧ 利用根的判别式解有关抛物线
与x轴两交点间的距离的问题。
⑨当
时，抛物线开口向上，当
时，抛物线开口向下。
一元三次方程
在特殊形式的一元三次方程
中，其判别式为
。当
时，有一个实根和两个复根；
时，有三个实根，当
时，有一个三重零根，
时，三个实根中有两个相等；
时，有三个不等实根。
在一般形式的一元三次方程
中，一般采用盛金判别法，即
令
当
时，方程有一个三重实根。
当
时，方程有一个实根和一对共轭虚根。
当
时，方程有三个不相等的实根。
参考资料
[1]
判别式的解释|判别式的意思|汉典“判别式”词语的解释[引用日期2022-05-17 21:34:32]
