偏心率(描述圆锥曲线轨道形状的数学量)

VLoG
次浏览
更新时间:2023-07-14
小编整理:
偏心率,描述圆锥曲线轨道形状的数学量,定义为曲线到定点(焦点)的距离与到定直线(准线)的距离之比。 对于椭圆,偏心率即为两焦点间的距离(焦距,2c)和长轴长度(2a)的比值,即e=c/a(偏心率一般用e表示)。 偏心率是用来描述圆锥曲线轨道形状的数学量,它不仅可以用于描述椭圆的形状,还可以用于描述其他圆锥曲线的形状,如双曲线和抛物线。 在圆锥曲线的研究和应用中,偏心率是一个非常重要的参数,它不仅可以用于研究曲线的几何性质,还可以用于解决与圆锥曲线相关的问题。 因此,对于圆锥曲线的研究和应用来说,掌握偏心率的概念和计算方法是非常重要的。偏心率
描述圆锥曲线轨道形状的数学量
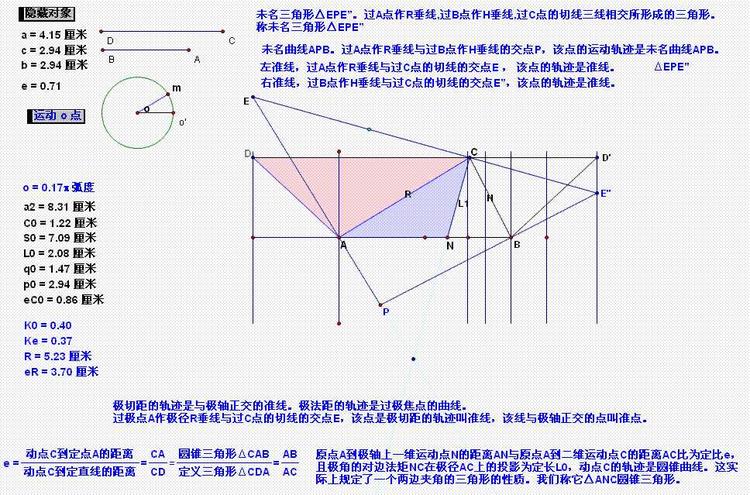
偏心率(Eccentricity)是用来描述圆锥曲线轨道形状的数学量,定义为曲线到定点(焦点)的距离与到定直线(准线)的距离之比。对于椭圆,偏心率即为两焦点间的距离(焦距,2c)和长轴长度(2a)的比值,即e=c/a(偏心率一般用e表示)。
基本信息
中文名
离心率
外文名
Eccentricity
别名
偏心率
当e=0时
圆
当e=1时
抛物线
0e1时
椭圆
当e1时
双曲线
通用表示字母
e
概念
偏心率(离心率)

椭圆两焦点间距离和长轴长度的比值。即某一椭圆轨道与理想圆环的偏离,长椭圆轨道“偏心率”高,而近于圆形的轨道“偏心率”低。
离心率定义为椭圆两焦点间的距离和长轴长度的比值。
椭圆的

抛物线的

圆的

行星的偏心率
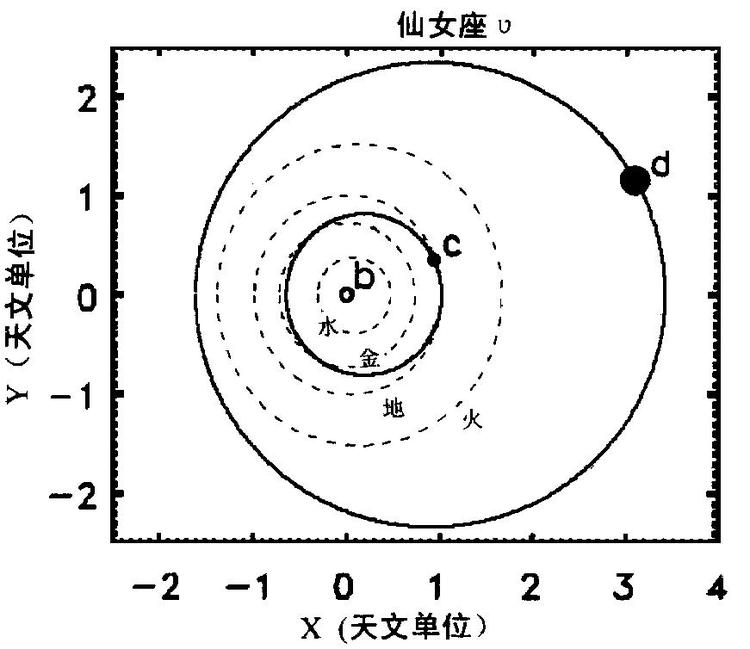
2.太阳和行星的矢径在相等的时间间隔中扫过相等的面积。
3.行星的轨道周期的平方与它的轨道的长轴的三次方成正比。
开普勒定律基于纯几何学推断,它们描述了一个单一质点绕一个固定中心的运动。它遵循牛顿第二定律以及牛顿万有引力定律。尽管开普勒定律阐明的是行星绕太阳的轨道运动,它们可以用于任意二体系统的运动,如地球和月亮,地球和人造卫星等。
其中p为半参量,而e为偏心率。
数据
太阳系八大行星的轨道偏心率
如下:
行星 偏心率
水星 0.205627
金星 0.006811
地球 0.016675
火星 0.093334
木星 0.048912
土星 0.053927
天王星 0.043154
海王星 0.01125
注:偏心率(即离心率

由上面数据可知,行星的偏心率与距日远近应该没有直接联系,而主要是由入射初始条件决定。








