变分原理(物理学的基本原理)

VLoG
次浏览
更新时间:2023-07-18
小编整理:
变分原理是物理学中的一条基本原理,它以变分法来表达。根据科内利乌斯·兰佐斯的说法,任何可以用变分原理来表达的物理定律描述一种自伴的表示。这种表示也被说成是厄米的,它描述了在厄米变换下的不变量。菲利克斯·克莱因的爱尔兰根纲领试图鉴识这类在一组变换下的不变量。 变分原理在物理学中有着重要的应用。例如,在最小作用量原理中,它被用来描述物理系统的演化。在这个原理中,物理系统的演化被定义为使得作用量最小的路径。这个原理在量子力学、经典力学和统计物理学中都有广泛的应用。 此外,变分原理还在量子力学中的薛定谔方程中起着重要的作用。薛定谔方程是一个本征值问题,它的解是一组本征函数,这些本征函数构成了一个完备的基组。在这个基组上,物理系统的哈密顿算子可以表示成一个本征值问题,这个本征值问题的解就是系统的能级和波函数。 总的来说,变分原理是物理学中的一条重要原理,它在描述物理系统的演化、量子力学中的本征值问题等方面都有着广泛的应用。变分原理
物理学的基本原理

变分定义
函数的微分定义式为f(x+Δx)-f(x)=f'(x)Δx+o(x);那么泛函的微分有类似的定义:Φ(γ+h)-Φ(γ)=F+R,此处F为h的函数,R=o(h^2).注意,这里和微分不同的是h不一定是无穷小量。
基本简介
设有一个体系,其中能量的有关条件已知,换句话说,已经知道体系的哈密顿算符H。如果不能解薛定谔方程来找出波函数,可以任意猜测一个归一化的波函数,比如说φ,结果是根据猜测的波函数得到的哈密顿算符的期望值将会高于实际的基态能量。变分原理是变分法的基本原理,用于量子力学和量子化学来近似求解体系基态。
变分定理
泛函
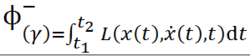
是可微的,其微分(变分)是
参考文献:
1)钱伟长,《变分法及有限元(上册)》,科学出版社, 1980年8月第一版
2)Shen Xiaoming(沈孝明),Mixed Compatible Element and Mixed Hybrid Incompatible Element Variational Methods in Dynamic of Viscous Barotropic Fluids,Proceedings ofthe second international confernce on fluid mechanics(Bejing,1993):511-516;
APPLIED MATHEMATICS AND MECHANICS(English Edition),Vol.15,No.6,JUN.1994:561-569
3)沈孝明,粘性流动的最大功率消耗原理不成立——论自然条件不参加变分兼论变分的定义和运算法则,北京大学学报,1990,26(3):291-293
4)Shen Xiaoming(沈孝明),Deformation Power and Complementary Power and so Forth of Compressible Viscous Fluid Floows and Their Applications in Variational Principles,《Some new trends on fluid mechanics and theoretical physics》,Chair man of Editiorial commitee:C.C.Lin(林家翘),Peking UnivercityPress,Frist Edition 1993:305-307
5)沈孝明,粘性流体动力学有限元变分原理,上海力学,1997,18(3):201-206
6)沈孝明,非线性弹性体大变形问题的新广义变分原理,上海力学,1988,9(4):66-72
外部链接
1.Venables, John, "The Variational Principle and some applications". Dept of Physics and Astronomy, Arizona State University, Tempe, Arizona (Graduate Course: Quantum Physics)2.Williamson, Andrew James, "The Variational Principle-- Quantum monte carlo calculations of electronic excitations". Robinson College, Cambridge, Theory of Condensed Matter Group, Cavendish Laboratory. September 1996. (dissertation of Doctor of Philosophy)3.Tokunaga, Kiyohisa, "Variational Principle for Electromagnetic Field". Total Integral for Electromagnetic Canonical Action,
Canonical Theory of Electromagnetics, Chapter VI


