转动惯量（物体绕轴转动时惯性的量度）

VLoG

次浏览

更新时间：2023-07-18

小编整理：

转动惯量是物体绕轴转动时惯性的量度，它是经典力学中一个非常重要的概念。了解物体的转动惯量可以让我们更好地预测物体在旋转运动中的行为。转动惯量的SI单位是kg·m²，表示物体对于转轴的转动惯性的大小。对于一个质点，转动惯量I等于质量m与质点到转轴垂直距离r的平方的乘积，即I=mr²。转动惯量是一个非常重要的物理量，在许多领域都有应用，例如机械工程、航空航天工程等。通过了解物体的转动惯量，我们可以更好地设计和控制物体的旋转运动，以达到更好的效果。

转动惯量

物体绕轴转动时惯性的量度

转动惯量(Moment of Inertia)，又称质量惯性矩，简称惯距，是经典力学中物体绕轴转动时惯性的量度，常用用字母I或J表示。转动惯量的SI单位为kg·m²。对于一个质点，I=mr²，其中，m是其质量，r是质点和转轴的垂直距离。

基本信息

中文名

转动惯量

外文名

Moment of Inertia

表达式

I=mr²

应用学科

物理学

适用领域范围

土木工程、机械工程

适用领域

刚体动力学

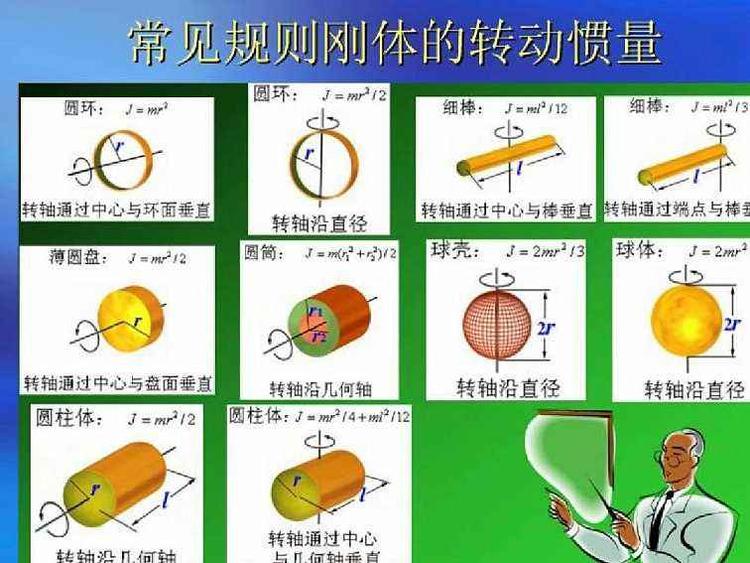
基本简介

转动惯量是刚体转动时惯性的量度，其量值取决于物体的形状、质量分布及转轴的位置。刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。

电磁系仪表的指示系统，因线圈的转动惯量不同，可分别用于测量微小电流或电量，譬如检流计、冲击电流计等。在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上，精确地测定转动惯量，都是十分必要的。

对于质量分布均匀，外形不复杂的物体，可以从其外形尺寸、质量分布用公式计算出相对于某一确定转轴的转动惯量。对于几何形状简单、质量分布均匀的刚体可以直接用公式计算出它相对于某一确定转轴的转动惯量。而对于外形复杂和质量分布不均匀的物体只能通过实验的方法来精确地测定物体的转动惯量，因而实验方法显得更为重要。

动力学公式

下面先给出一些（定轴转动的）刚体动力学公式。

角加速度与合外力矩的关系：

，式中，M为合外力矩，β为角加速度。

可以看出这个式子与牛顿第二定律具有类似的形式。

角动量：

刚体的定轴转动动能：

注意：这只是刚体绕定轴的转动动能，其总动能应该再加上质心平动动能。由这一公式，可以从能量的角度分析刚体动力学的问题。

张量定义

刚体绕某一点转动的惯性可由惯性张量描述。惯性张量是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。为了清晰，这里仅给出绕质心的转动惯量张量的定义及其在力矩方程中的表达式。

设有一个刚体A，其质心为C,刚体A绕其质心C的转动惯量张量

定义为：

该积分遍及整个刚体A，其中，

，是刚体质心C到刚体上任一点B的矢径；表达式

是两个矢量的并矢，而

为单位张量，

是一个典型的单位正交曲线标架；

是刚体的密度。

转动惯量张量的力矩方程：

设刚体A所受到的绕其质心C的合力矩矢量为：

，刚体A在惯性系下的角速度矢量为

，角加速度矢量为

，A绕其质心的转动惯量张量为

，则有如下的力矩方程：

将上面的矢量形式的力矩方程向各个坐标轴投影，或者，更确切地说，与各个坐标轴的单位方向矢量相点乘，就可以获得各个坐标轴分量方向的标量形式的力矩方程。

转动惯量张量

是一个二阶张量，虽然在标架

下它有九个分量，但是因为它是一个对称张量，故其实际独立的分量只有六个。

测定方法

测定刚体转动惯量的方法很多，常用的有三线摆、扭摆、复摆等。实验室中最常见的是三线摆法，该方法通过扭转运动测定物体的转动惯量，其特点是物理图像清楚、操作简便易行、适合各种形状的物体，如机械零件、电机转子、枪炮弹丸、电风扇的风叶等的转动惯量都可用三线摆测定。这种实验方法在理论和技术上有一定的实际意义。

实验原理

三线摆是在上圆盘的圆周上，沿等边三角形的顶点对称地连接在下面的一个较大的均匀圆盘边缘的正三角形顶点上。当上、下圆盘水平三线等长时，将上圆盘绕竖直的中心轴线转动一个小角度，借助悬线的张力使悬挂的大圆盘绕中心轴作扭转摆动。同时，下圆盘的质心O将沿着转动轴升降，H是上、下圆盘中心的垂直距离；h是下圆盘在振动时上升的高度；r是上圆盘的半径；R是下圆盘的半径；

是扭转角。

由于三悬线能力相等，下圆盘运动对于中心轴线是对称的，仅分析一边悬线的运动。用L表示悬线的长度，当下圆盘扭转一个角度α时，下圆盘的悬线点移动到，下圆盘上升的高度为，与其他几何参量的关系可作如下考虑。

实验内容

1）测定仪器常数。

恰当选择测量仪器和用具，减小测量不确定度。自拟实验步骤，确保三线摆的上、下圆盘的水平，使仪器达到最佳测量状态。

2）测量下圆盘的转动惯量，并计算其不确定度

转动三线摆上方的小圆盘，使其绕自身轴转一角度α，借助线的张力使下圆盘作扭摆运动，而避免产生左右晃动。自己拟定测的方法，使周期的测量不确定度小于其它测量量的不确定度。利用公式求出，并推导出不确定度传递公式计算的不确定度。

3）测量圆环的转动惯量

在下圆盘上放上待测圆环，注意使圆环的质心恰好在转动轴上，测量系统的转动惯量。测量圆环的质量和内、外直径。利用式求出圆环的转动惯量。并与理论值进行比较，求出相对误差。

4）验证平行轴定理

将质量和形状尺寸相同的两金属圆柱重叠起来放在下圆盘上，注意使质心与下圆盘的质心重合。测量转动轴通过圆柱质心时，系统的转动惯量。然后将两圆柱对称地置于下圆盘中心的两侧。测量此时系统的转动惯量。测量圆柱质心到中心转轴的距离计算，并与测量值比较。

相关定理

转动惯量详解及物理意义

先说一说转动惯量的由来，先从动能说起。大家都知道动能

，而且动能的实际物理意义是：物体相对某个系统运动的实际能量。

把

代入

，式中，w是角速度，r是半径。

在这里对任何物体来说是把物体微分化分为无数个质点，质点与运动整体的重心的距离为r，而再把不同质点积分化得到实际等效的r，得到

。

由于某一个对象物体在运动当中的本身属性m和r都是不变的，所以把关于m、r的变量用一个变量K代替,

，得到

，K就是转动惯量。

平行轴定理

一个物体以角速度ω绕固定轴z轴的转动同样可以视为以同样的角速度绕平行于z轴且通过质心的固定轴的转动。也就是说，绕z轴的转动等同于绕过质心的平行轴的转动与质心的转动的叠加。

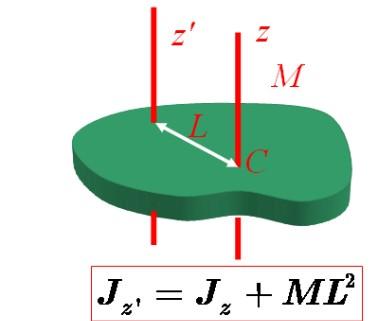
利用平行轴定理可知，在一组平行的转轴对应的转动惯量中，过质心的轴对应的转动惯量最小。垂直轴定理一个平面刚体薄板对于垂直它的平面轴的转动惯量，等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。

表达式:

转动惯量的量纲为L2M，在SI单位制中，它的单位是

。刚体绕某一点转动的惯性由更普遍的惯量张量描述。惯量张量是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。

垂直轴定理

一个平面刚体薄板对于垂直它的平面的轴的转动惯量，等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和，这就是垂直轴定理。

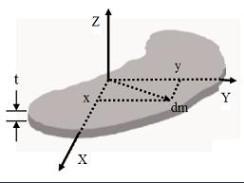
垂直轴定理的表达式为：

式中，

分别代表刚体对x,y,z三轴的转动惯量。

对于非平面薄板状的刚体，亦有如下垂直轴定理成立：

利用垂直轴定理可对一些刚体对一特定轴的转动惯量进行较简便的计算。

刚体对一轴的转动惯量，可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。由此折算所得的质点到转轴的距离，称为刚体绕该轴的回转半径κ，其公式为

，式中，M为刚体质量；I为转动惯量。

除以上两定理外，常用的还有伸展定则。伸展定则阐明，如果将一个物体的任何一点，平行地沿着一支直轴作任意大小的位移，则此物体对此轴的转动惯量不变。可以想像，将一个物体，平行于直轴地，往两端拉开。在物体伸展的同时，保持物体任何一点离直轴的垂直距离不变，则伸展定则阐明此物体对此轴的转动惯量不变。伸展定则通过转动惯量的定义式就可以简单得到。