向心加速度(力的作用使物体产生的加速度)

VLoG
次浏览
更新时间:2023-07-18
小编整理:
向心加速度(centripetal acceleration)是作曲线运动的物体加速度在指向曲线法向方向上的分量。它可以被理解为一个物体在圆周运动时,指向圆心的外力或外力指向圆心的分力。这个向心加速度的作用是改变物体的运动方向,使其沿着圆的切线方向运动。 向心加速度的概念常被用于物理学和工程学中,特别是在处理关于物体运动和力学的问题时。它也可以在力学、光学、电磁学等领域中发挥作用。 在数学上,向心加速度可以通过向心力的大小和物体的质量来计算。它也可以被表示为一个向量,其大小等于向心力的大小,方向指向圆心。 总之,向心加速度是物体在圆周运动时产生的加速度,它指向圆心的方向,是物体运动方向改变的原因。向心加速度
力的作用使物体产生的加速度

概述
物体做圆周运动时,沿半径指向圆心方向的外力(或外力沿半径指向圆心方向的分力)称为向心力。
由牛顿第二定律,力的作用会使物体产生一个加速度。向心力产生的加速度就是向心加速度,方向指向圆心。可理解为做圆周运动物体加速度在指向圆心方向上的分量。
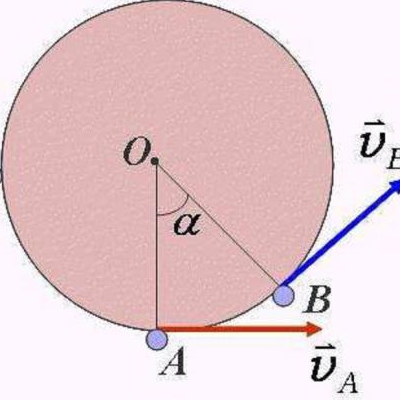
如图1所示,所有做曲线运动的物体都有向心加速度,向心加速度反映速度方向变化的快慢。
公式
向心加速度公式为:

由牛顿第二定律,力的作用会使物体产生一个加速度。合外力提供向心力,向心力产生的加速度就是向心加速度。可能是实际加速度,也可能是物体实际加速度的一个分加速度。
方向
所有做曲线运动的物体都有向心加速度,向心加速度反映的是圆周运动在半径方向上的速度方向改变的快慢。
向心加速度又叫法向加速度,意思是指向曲线的法线方向的加速度。
向心加速度的方向始终与速度方向垂直,也就是说线速度始终沿曲线切线方向。
难点突破
高一物理《曲线运动》中的“向心加速度”,既是教材的重点,也是教材的难点。
1)了解和掌握学生的思维障碍
只有认真研究和探索学生在学习“向心加速度”中的困难所在,然后才能做到有的放矢,对症下药。
在本节内容的学习中,学生的疑难点主要有二:一是“既然匀速圆周运动的速度大小不变,却又具有加速度,不好理解”。二是“既然加速度方向指向圆心,物体何不向圆心运动?”学生之所以会产生这样的疑问,是有其认识根源的。
其一,学生对变速直线运动记忆犹新,尤其对该运动中“加速度导致速度大小的改变”印象更为深刻。他们立足于已有的知识和经验来看待匀速圆周运动的加速度,于是难免以老框框套新问题,这种思维定势的负迁移作用,使他们的思维限制在已有的运动模式之中而忽视了问题的不同本质。
其二,学生在此之前虽学习了平抛、斜抛运动,但主要是侧重于运动的合成和分解知识的应用,至于抛体的速度方向何以会时刻改变,它与加速度有怎样的关系,书中并未详述,学生没有建立起较为清晰的模式。他们多数仅仅是从经验出发,被动地接受“物体受到跟速度方向成角度的重力,所以做曲线运动”这一事实。因此可以说他们是在知识准备不足,思维想象无所模拟的情况下来接受新知识的。于是一旦接触到圆周运动,就表现为不能顺应,对于向心加速度感到很抽象,甚至不可思议。
如果我们能在教学之始就注意到这些因素,以指导自己从学生的实际出发,采取相应的方式和方法,对于学生理解和掌握向心加速度的概念,就会收到事半功倍之效。
2)类比引导,确认加速度的存在
如何使学生确认匀速圆周运动具有加速度,这是教学中的一个重要环节。笔者的做法是,排除变速直线运动这一思维定势的干扰,用斜上抛运动“搭桥”—一利用斜上抛和圆周运动的速度方向时刻改变这一共性,引导启发学生通过相似联想,从而确认向心加速度的存在。
讲匀速圆周运动时,应指出一定存在一个使速度方向时刻改变的加速度,否则质点就要沿切线方向飞出而做直线运动,也就顺理成章了。
3)分析推理,确定加速度的方向
在学生已初步认识到匀速圆周运动质点具有使速度方向时刻改变的加速度的基础上,怎样进一步使学生心悦诚服地接受向心加速度的方向“在任一点都沿着半径指向圆心”这一结论,是教学中的又一个环节。
首先,赖于学生对物体做曲线运动的条件的了解,结合上述斜上抛运动速度方向的改变原因,让学生分析得出“向心加速度的方向必指向圆内”,此乃第一步;继而抓住匀速圆周运动的“速度大小不变,方向改变”这一重要特征,启发学生分析思考,欲满足这一条件,则必然在速度方向上没有加速度分量,结合示图得出,“向心加速度在任何一点必定和速度垂直”的结论,此乃第二步;第三步,匀速圆周运动的轨迹是圆,速度方向总沿着圆的切线方向,垂直于切线的只能是圆的半径。由以上三个特点得出:“质点做匀速圆周运动时,它在任一点的加速度都是沿着半径指向圆心”。故此称为“向心加速度”。
至此,学生对向心加速度的存在及其方向的认识和理解,就不再感到空洞和模糊,而是较为充实和清晰了。
至于向心加速度公式的推导,由于学生的思维已从单纯的抽象概念转变到较能把握住的明晰的空间形象,因此不论是用矢量三角形或其它途径推导公式,学生均不感到困难。笔者的做法是,导出加速度方向后,让学生自己阅读课文,引导和指点他们自己按课本所述矢量三角形法推导出向心加速度公式。
思维误区
2)据公式


















