问题

倍立方问题

要想遏止瘟疫，得将阿波罗神殿中那正立方的祭坛加大一倍。人们便把每边增长一倍，结果体积当然就变成了8倍，瘟疫依旧蔓延；接着人们又试着把体积改成原来的2倍，但形状却变为一个长方体……第罗斯岛人在万般无奈的情况下，只好鼓足勇气到雅典去求救于当时著名的学者柏拉图。

开始，柏拉图和他的学生认为这个问题很容易。他们根据平时的经验，觉得利用尺规作图可以轻而易举地作一个正方形，使它的面积等于已知正方形的2倍，那么作一个正方体，使它的体积等于已知正方体体积的2倍，还会难吗？结果，……但是，柏氏门徒当时倒有两件差点成功的作法：

注解

注：『求体积是稜长 a 的立方体的2倍的立方体』，这问题可以转化为『求在 a 与 2a 之间插入二数x,y，使 a,x,y,2a 成等比数列』 即 

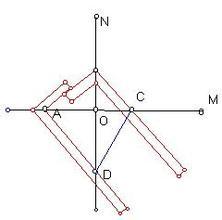
( 则 ) 作法： 1. 作互相垂直的线M,线N,交点为O；2. 在M上取 

作法： 1. 作互相平形且距离为2a的直线M,

3. [以下是西元前350年希腊数学家梅内克缪斯Menaechmus)的作法] 已知：线段 a 求作：线段x,y，使得