开普勒第三定律(行星运动三定律之一)

VLoG
次浏览
更新时间:2023-05-20
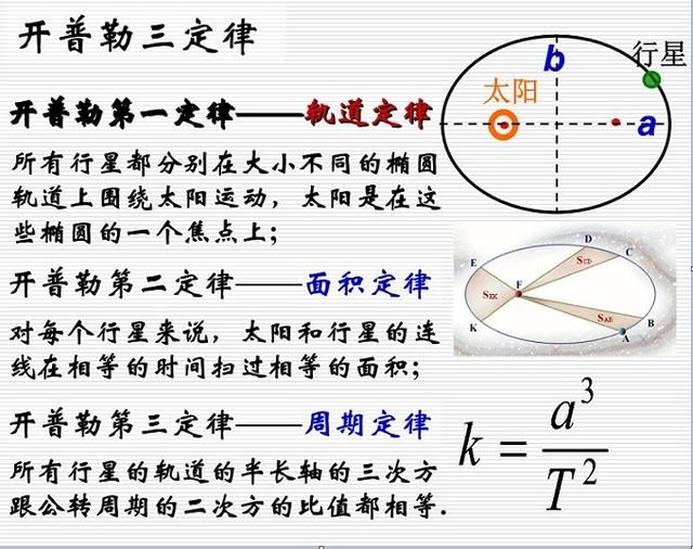
定律定义
推导过程
观测数据
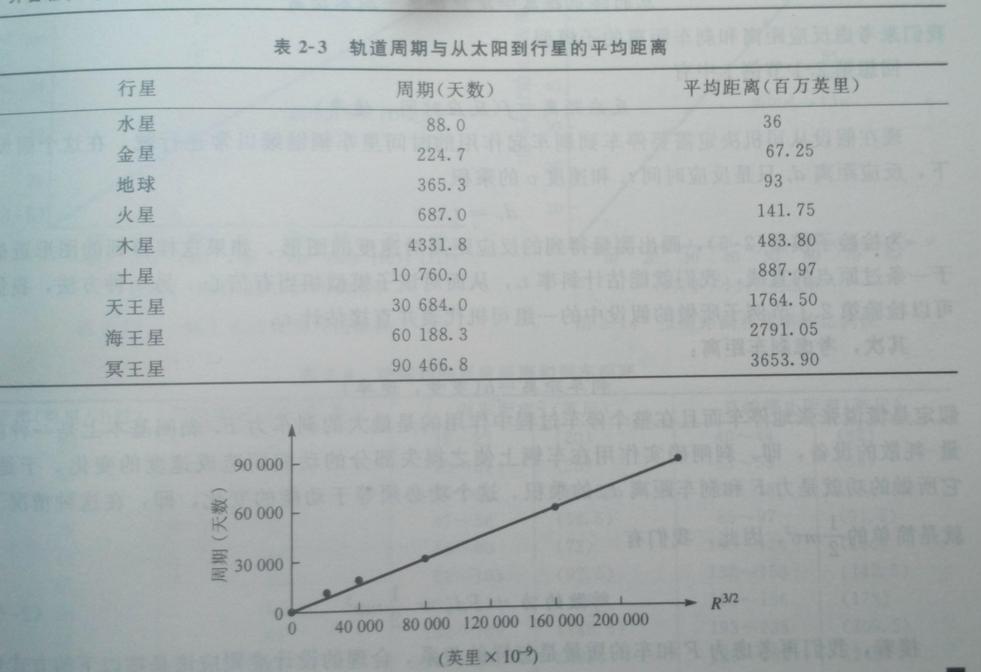
开普勒的原始数据
常规方法
方法一:
现实中的星体运动的轨道大多数是椭圆,于是便有以下推导:
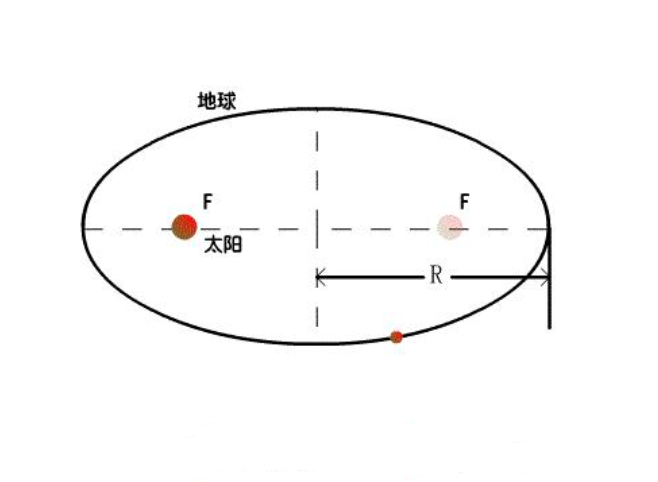
R为半长轴


面积速度为

选近日点A和远日点B来研究,由ΔS相等可得


得 :

由几何关系得: ,
,  ,
,



所以



整理得 。
。

方法二:
则周期 (1)
(1)

(2)式得

(2)式代入(1)式得  (3)
(3)

根据椭圆的性质,椭圆的半短轴 ,则
,则 (4)
(4)


式(4)代入(3)式得 ,由此式可知绕同一中心天体运行的人造星体轨道半长轴的三次方跟它们的公转周期的二次方的比值由中心天体的质量所决定。
,由此式可知绕同一中心天体运行的人造星体轨道半长轴的三次方跟它们的公转周期的二次方的比值由中心天体的质量所决定。

适用范围
应用实例
天体
实际星体问题大多数为二体问题,实际应用时,人们把开普勒定律看成是牛顿定律和万有引力定律的表现形式。(M为中心天体质量,m为行星质量)
在 时,可以认为
时,可以认为 ,这就是开普勒定律的第三表达式,其中
,这就是开普勒定律的第三表达式,其中 为开普勒常数。
为开普勒常数。



由此可见,开普勒定律只是一个近似定律。
通过开普勒第三定律,在天体运行中有以下应用:
2.通过两绕同一中心天体运动的行星的公转周期,算出这两行星分别到中心天体的平均距离。(因实际轨道为椭圆形,故采用平均距离)。
3.在星—箭分离问题中,通过星箭椭圆运动周期之比,计算星箭运动轨迹半长轴之比。
二体问题是天体力学中的一个基本问题,它是指可视为质点的两个天体在相互间唯一的万有引力作用下的运动规律问题。二体问题可以用牛顿万有引力定律和牛顿运动定律来描述并得到完全解决。开普勒三定律是二体问题的解。
航天
开普勒轨道的定义:
1.符合开普勒三定律的天体或航天器的运行轨道;
2.由二体问题的解的道德天体或航天器的运行轨道。
由定义可知,开普勒的轨道也称为二体问题轨道,符合上述定义的开普勒轨道也称为理想的开普勒轨道。航天器的开普勒轨道可由如下二体问题的基本方程解得:

发展简史

约翰尼斯开普勒
1600年,德国天文学家开普勒应丹麦天文学家第谷之邀,开普勒前往布拉格做第谷的助手。次年,第谷去世,他将自己一生积累的观测资料留给了开普勒。
开普勒分析第谷测量行星位置的多年记录(特别是火星的椭圆形轨道),在1619年发表他的第三行星定律。
定律影响
相关合集

开普勒三大定律
共3个词条938阅读
开普勒第一定律
1618年开普勒提出的定律
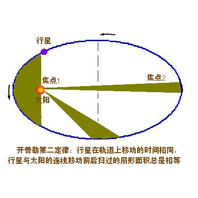
开普勒第二定律
三条开普勒定律之一
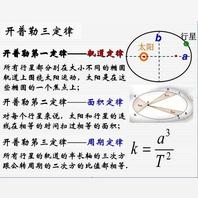
开普勒第三定律
行星运动三定律之一
查看更多














































