开普勒第二定律（三条开普勒定律之一）
VLoG
次浏览
更新时间：2023-05-20
开普勒第二定律
三条开普勒定律之一
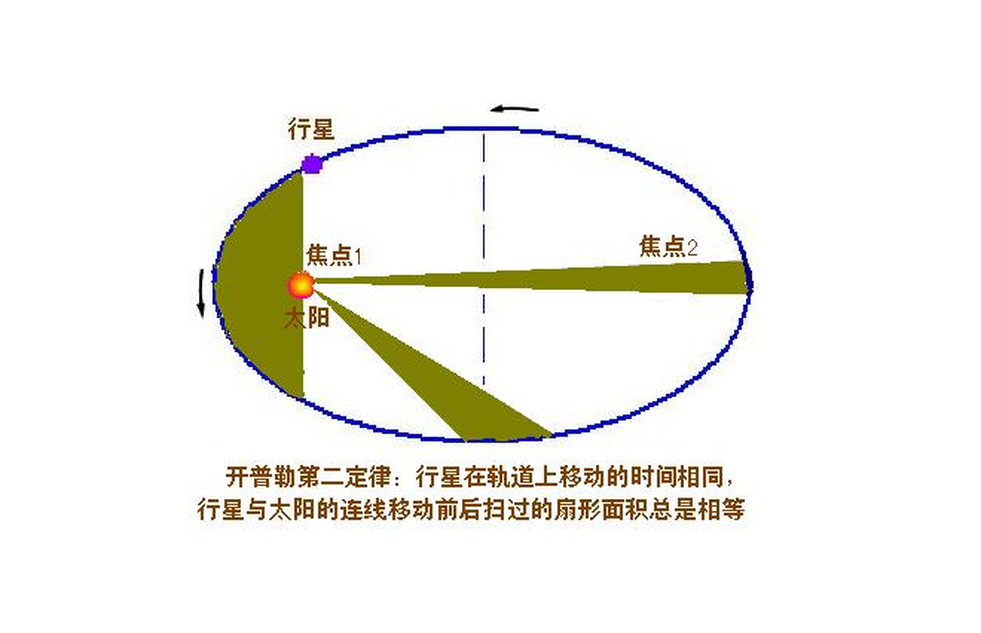
定律定义
数学推导
由一式可以看出，这一定律实际揭示了行星绕太阳公转的角动量守恒。
定律要素
适用范围
局限性
1915年，爱因斯坦根据广义相对论把行星的绕日运动看成是它在太阳引力场中的运动，由于太阳的质量造成周 围空间发生弯曲，使行星每公转一周近日点进动为：其中a为行星轨道的长半轴，c为光速，以cm/s表示，e为偏心率，T为公转周期。对于水星，计算出
。
2.对于具有极大能量的天体，如类星体，现有的开普勒第二定律显然不适用。
衍生推论
1.设行星1和行星2运行轨道的半径分别为
和
，当小于时。
则有
（1）行星1的线速度大于行星2的线速度；
（3）行星1的加速度大于行星2的加速度 ；
（4）行星1的运行周期小于行星2的运行周期 ；
（5）在相同的时间内，行星1的运行路程大于行星2的运行路程 ；
（6）在相同的时间内，行星1扫过的角度大于行星2扫过的角度。
拓展形式
数据：两倍掠面速度(J)，两倍椭圆面积(
)，椭圆周期定律(T)，极径(R)，偏斜速度(V)，偏斜动量(mV)，速度方向与极径夹角(α)，球面速度(V)，极径角速度(ωR), 弧高(RL) ，最小曲率半径（L），速度系数（V），天体引力常数（GM）
开普勒第二定律掠面速度守恒公式：
这是天体偏斜运动一般的矢积面速度守恒公式：极径*天体速度*两矢夹角正弦。
开普勒第二定律几种表述：
表述一：
J= 
= 
= 
表述二：极径(R)* 天体速度(VS)*两矢夹角的正弦sin(α)的三个变量的积是不变量。
表述三：天体速度(V)*弧高(RL) 二个变量的积是不变量。
表述四：极径(R)*球面速度(V)二个变量的积是不变量。
表述五：极径的平方(R²)*极径角速度(ωR)的积是不变量。
表述六：最小曲率半径（L）*速度系数（V）。
表述七：天体引力常数（GM）与最小曲率半径（L）积的平方根。
特别的：
近日点的天体速度最大： 
远日点的天体速度最小：
。
发展简史
丹麦天文学家第谷·布拉赫死后，留下20多年的观测资料和一份精密星表。第谷提出了一种介于地心说和日心说之间的学说，在17世纪传入我国，并产生重大影响。在没有天文望远镜的情况下，第谷对天体方位进行了几十年的观测，凭借着惊人的毅力和耐心，积累了大量的精确材料，开普勒的发现，就是通过归纳分析这些材料得出的。
开普勒认为通过对第谷的记录做仔细的数学分析可以确定哪个行星运动学说正确的：哥白尼日心说，古老的托勒密地心说，或者是第谷本人提出的第三种学说。但是经过多年仔细的计算和研究，他发现这三种学说与第谷的星表和观测数据都不符合。
约翰内斯·开普勒
当开普勒继续研究时，“诡谲多端”的火星又将他骗了。原来，开普勒和前人都把行星运动当作等速来研究的。他按照这一方法苦苦计算了1年，却仍得不到结果。后来他发现，火星运行速度是不匀的，当它离太阳较近时运动得较快(近日点),离太阳远时运动得较慢(远日点)。
开普勒发现该问题后，经过精准刻苦的计算，他发现：在椭圆轨道上运行的行星速度不是常数，而是在相等时间内，行星与太阳的连线所扫过的面积相等。这就是行星运动第二定律，又叫“面积定律”。
这两条定律刊布在1609年出版的《新天文学》(又名《论火星的运动》)中，该书还指出两定律同样适用于其他行星和月球的运动。
应用领域
开普勒第二定律，或者是用几何语言，或者是用方程，将行星的坐标及时间跟轨道参数相连结。有效解决了对于天体运动规律的解释。在研究天体的运动中，利用牛顿的力学和开普勒三大定律的有效结合，可以预测天体的运行轨道、运动速度、旋转周期，从而能够预测某一时刻到天体在空间中的位置，能够应用到天体探测、卫星发射等领域。
定律影响
首先，开普勒定律在科学思想上既有重要影响。其表现出的无比勇敢的创造精神和质疑精神激励着后来的学者们勇于创新，勇于质疑。
第三，包括开普勒第二定律在内的开普勒定律使人们对行星运动的认识得到明晰概念。它证明行星世界是一个匀称的、可以计算的系统。太阳位于每个行星轨道的焦点之一。行星公转周期决定于各个行星与太阳的距离，与质量无关。
第四，开普勒第二定律有力的证明了日心说，进一步推翻了神创论，弘扬了科学精神，推动了时代发展。为后来牛顿万有引力的提出奠定了基础，提供了有力论据。
相关合集
开普勒三大定律
共3个词条938阅读
开普勒第一定律
1618年开普勒提出的定律
开普勒第二定律
三条开普勒定律之一
开普勒第三定律
行星运动三定律之一
查看更多
