平面向量(物理学中定理定律)

VLoG
次浏览
更新时间:2023-05-20
平面向量
物理学中定理定律

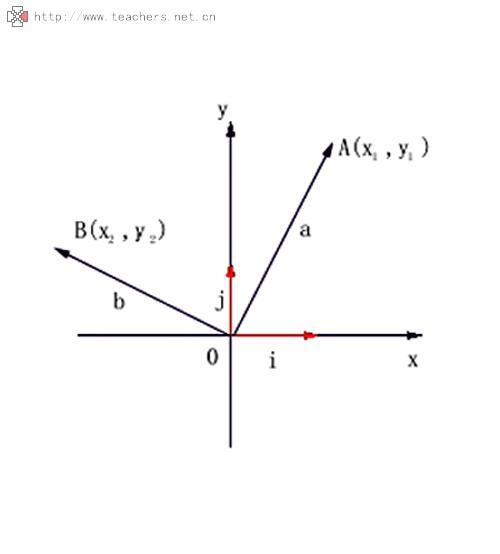
平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量,物理学中也称作矢量,与之相对的是只有大小、没有方向的数量(标量)。平面向量用a,b,c上面加一个小箭头表示,也可以用表示向量的有向线段的起点和终点字母表示。
发展历程
相关概念
表示方法
几何表示
具有方向的线段叫做有向线段,我们以A为起点、B为终点的有向线段作为向量,可以记作 。但是,区别于有向线段,在一般的数学研究中,向量是可以平移的。
。但是,区别于有向线段,在一般的数学研究中,向量是可以平移的。

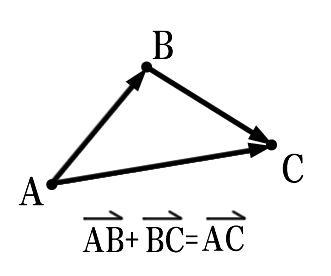
运算性质
减法


数乘
实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作 。当
。当 时,
时, 的方向和a的方向相同,当
的方向和a的方向相同,当 时,
时, 的方向和a的方向相反,当
的方向和a的方向相反,当 时,
时, 。
。







用坐标表示的情况下有:

设λ、μ是实数,那么满足如下运算性质:
1.

2.

3.

4.

5.

数量积
已知两个非零向量a、b,那么 (θ是a与b的夹角)叫做a与b的数量积或内积,记作
(θ是a与b的夹角)叫做a与b的数量积或内积,记作 。零向量与任意向量的数量积为0。数量积a·b的几何意义是:a的长度
。零向量与任意向量的数量积为0。数量积a·b的几何意义是:a的长度 与b在a的方向上的投影
与b在a的方向上的投影 的乘积。
的乘积。




两个向量的数量积等于它们对应坐标的乘积的和。即:若 ,则
,则


数量积具有以下性质:
1.

2.

3.

4.

5.

6.

7.

向量积
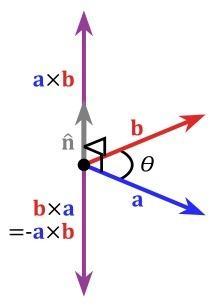
向量积示意图






若a、b不共线, 是一个向量,其模是
是一个向量,其模是 ,
, 的方向为垂直于a和b,且a、b和
的方向为垂直于a和b,且a、b和 按次序构成右手系。若a、b共线,则
按次序构成右手系。若a、b共线,则 。
。







向量积具有如下性质:
1.

2.

3.

4.

5.

基本定理
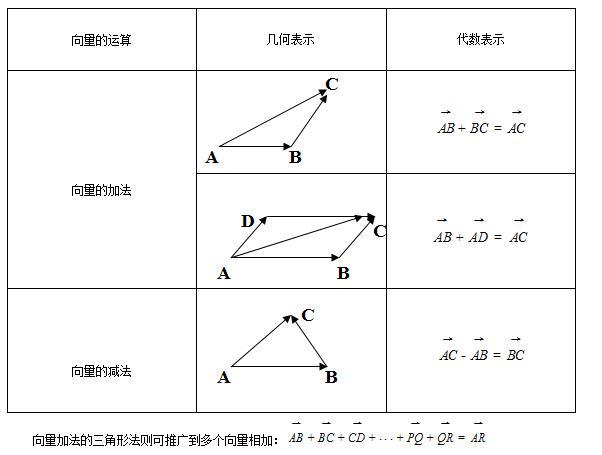
平面向量

有关推论
•三角形ABC内一点O, ,则点O是三角形的垂心。
,则点O是三角形的垂心。

•若O是三角形ABC的外心,点M满足 ,则M是三角形ABC的垂心。
,则M是三角形ABC的垂心。

•若O和三角形ABC共面,且满足 ,则O是三角形ABC的重心。
,则O是三角形ABC的重心。

•平面三角形ABC内有一点O,则S