屈光度(屈光力的大小单位)

VLoG
次浏览
更新时间:2023-05-22
屈光度
屈光力的大小单位

基本信息
| 中文名 | 屈光度 |
| 外文名 | Dioptre(英),Diopter(美) |
| 属性 | |
| 大小单位 | 屈光力 |
| 单位 | D |
简介
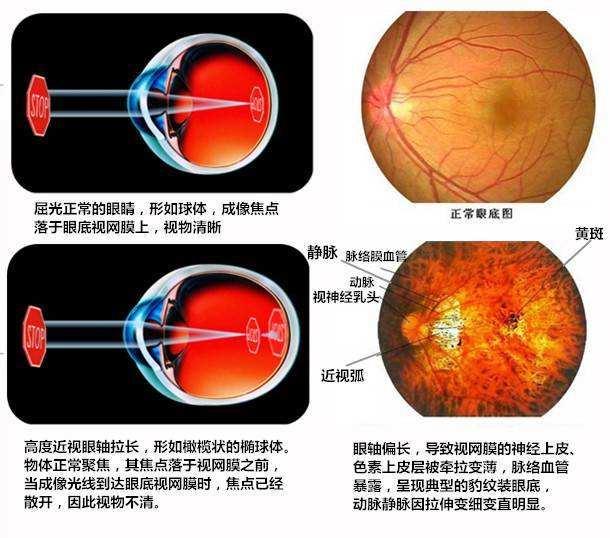
屈光度
眼睛折射光线的作用叫屈光,用光焦度来表示屈光的能力,叫做屈光度。眼睛不使用调节时的屈光状态,称为静态屈光,标准眼静态屈光的光焦度+58.64D。人眼在使用调节时的屈光状态,称为动态屈光,其光焦度强于静态屈光的光焦度。由于眼睛屈光度不正确,造成不能准确在视网膜成像,就是视力缺陷,一般情况需要佩带眼镜,通过镜片补充和矫正眼睛本身的屈光度,达到视网膜正确成像的目的!
焦距f的长短标志着折光能力的大小,焦距越短,其折光能力就越大,近视的原因就是眼睛折光能力太大,远视的人则折光能力太弱。
焦距的倒数叫做透镜焦度,或屈光度,用φ表示。如果焦距是10cm,那么φ=10D。
一个+3屈光度的透镜,会把平行的光线聚焦在镜片的1/3米外。
屈光度的单位简写是D,国际单位制的单位是 m的-1次方。
一般眼镜常使用度数来表示屈光度,以屈光度 D 的数值乘以 100 就是度数[1] ,例如 -1.0D 等于近视眼镜(凹透镜)的 100度。
检查
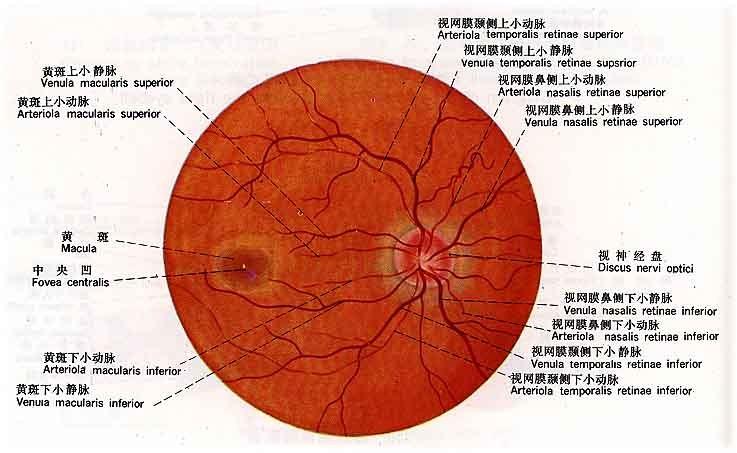
屈光度
自动验光仪验光法
用自动检查仪代替检查者手里拿的视网膜镜和各种镜片。
计算
屈光力越强,焦距越短。2D屈光力的透镜焦距为1/2m或50cm。如果想知道透镜的焦距,用100cm,也就是1.00m除以屈光力,结果即为焦距。例如,5D屈光力的焦距为20cm。(100cm除以5D=20cm。)凸透镜的屈光力以“+”号表示,凹透镜的屈光力以“—”表示。 1 屈光度或 1D 等于常说的 100 度。
眼镜的度数=屈光度数×100
调节

相机的屈光度调节装置
作用
第一点
对于同种材料制成的凸透镜,其凸度越大,屈光度数越大,反之越小。换言之,对同一只眼球而言,近视度

眼镜度数检测
第三点
由于普通眼镜与眼球相分离,形象直观,容易计算。本节探讨的重点是眼镜对眼球屈光的影响,对有关眼镜的论述,都是针对普通眼镜。戴角膜接触镜与普通眼镜在屈光方面具有相同的效果,其原理和技术在眼镜行业已经很成熟,因此不再论述。
第四点
在屈光学中,只有在某些特殊情况下,屈光度数为P1、P2两透镜组合产生的屈光效果才是屈光度为P1+P2的透镜。在眼球与透镜组成的光路中,在效果上或定性的计算中,也可以有P1+P2这种情况,这并非透镜组合后的实际屈光效果,而是一种简化和近似,因为眼睛具有自我改变屈光度的能力。虽然较难用实验验证,但从眼球的调节效果看,它应当具有抵消镜片屈光度的作用,而该公式却具有简化计算的作用。对于眼球和透镜所组成的系统来说,至多是两个透镜组成的屈光系统,因此可以利用屈光学理论进行计算。当戴上透镜时,因眼球特殊的调节作用,将透镜的屈光度和眼球调节适应后的屈光度相加减,也可得到近似值,虽然与准确地测量眼球的屈光力尚有一段距离,但在效果上却接近。在该论证中,尽管从理论上进行了推导,但实验和测量都非常困难,就象配制近视镜需要试戴一样,在用来指导配镜的过程中还要进行试验。
第五点
从眼球的屈光特点看,有人测得眼球的静屈光力为+58.6D,这虽然是一特例,但也基本反映出眼球具有很强
的屈光力,其调节相对较小,正常眼为0——10D左右,近视眼为n——10D(n指眼球的近视屈光度数)左右,而它又固定在眼眶内,因此对某一个人来说,可以认为眼球的屈光系统——“透镜”的中心到视网膜的距离不变,在以后的计算中,可认为像距为常数K,对于眼球的屈光来说,如果能在视网膜上成清晰的像,该屈光系统仍满足透镜成像公式
1/u+1/k=P
其中K是常数,P为眼球的屈光度数,是变量,意思是不同的人看不同距离的目标和不同的人眼球的屈光度数不同,U指目标到眼球的距离。该公式成立的条件是:某一时刻,眼睛看某一距离的目标,且目标在眼睛的近、远点之间。从公式看,正视眼看无穷远处时1/u=0,上式可化为P=1/K,可令1/k=P0,即P0为眼球的静屈光度。当看距眼球为L的目标时,“透镜”成像公式变为1/L+1/K=1/L+P0,1/L为眼球增加的屈光度数,1/L+P0即为眼球看距离为L的目标时的屈光度。
对于戴镜者来说,在一般情况下,眼球到眼镜中心的距离约为1.2——2.4CM,以下用h表示,但对于某人某一时刻的值是确定的,设屈光度为P'的透镜的焦距为F,当看距离为L的目标时,镜片成像公式如下:
1/L+1/V=P'==>1/V=P'-1/L①
此时透镜所成像到眼球这一“透镜”的距离为|V|+h,眼球的屈光情况满足公式:1/(|V|+h)+1/K=P②
从公式看,如果|V|比h大得多,根据①公式,②式可近似简化为:
1/|V|+1/K=D=|D'-1/L|+1/K③
从该公式看,|V|的大小取决于物距L和透镜的焦距,考虑到实际情况,近视眼镜的屈光度大多数大于-6D,学生看书、写字的距离大多大于0.25M,而且根据透镜成像公式可知,凹透镜屈光度数P'(注D'<0,下同)越小,V|越小,物距越小,|V|越小,如当D'=-5,U=0.25时,V|=0.111M,仍比0.02M大很多。所以作为理论

近视眼镜
第六点
误差分析。如果以公式为标准,那么产生误差的原因是多方面的,现对此分析。
(1)因为眼球的调节与形变同时进行,有调节就有形变,有形变就有眼球前后径的变化,还由于晶状体和角膜本身形变而导致的角膜、房水、晶状体所组成的“凸透镜”光心的变化。虽然近视或老视本身并不能说明其前后径的变化(一说,近视眼是眼球成像在视网膜前方,但近调节的过强或睫状肌不能放松都可实现这一点,不能充分说明眼球前后径变长),但更不能说明其不变性。这些因素的存在决定了公式中K只是一个近似,而且近调节幅度越大,K值变化越大,这是产生误差的一个原因。但考虑到在眼球调节中,晶状体的屈光度调节和眼球的屈光度(约60屈光度)相差很远,而眼球调节幅度一般少于10个屈光度,相对较小,角膜屈光度变化更小,因此,可认为“透镜”光心到视网膜的距离几乎不变。
(2)因每个人的眼球前后径不等,对不同的人而言,K并非常数,很难准确测量,但具体到某一个人的某一阶段而言,眼球前后径不变,可认为K是常数。
(3)对不同的人而言,眼镜片到“凸透镜”光学中心的距离是一较难测量的变量,这也影响到计算的准确性。由计算可知,h增大时,误差增大,反之越小。
第七点
在眼前放置透镜时,与正常眼相比,如果眼睛仍然能看清目标,从眼球的调节效果看,眼镜首先抵消眼球调节的不足,因此在以后的计算中,只要在眼球正常的调节范围内,用于抵消透镜的效果在理论上能够成立,我们无须注意眼球实际屈光度的变化。对眼球来说,不管戴多少屈光度的眼镜,要看清前面的目标,必须低消眼镜的作用而增加屈光度调节。
第九点
对于眼球和镜片所组成的屈光系统来说,镜片度数是确定的,而眼球的屈光度数却是个变量,因此,把眼球看成是一个可调凸透镜的意思是:眼睛透过眼镜能看清某一目标时,眼球的屈光度数确定,因而完全可以利用屈光学理论进行计算,但眼球看目标的距离发生变化时,其屈光度数也随之变化。
第十点
对眼球与眼镜组成的屈光系统而言,只有两个“透镜”组成,可看成一个等效的透镜组,透镜的度数可相加减,比如一个+5D的透镜,可看成是一个(+2D)+(+3D)的透镜组,虽然在多数情况下并不成立,但在理论为我们解决问题提供了方便。
参考资料
[1]
资料来源[引用日期2019-07-29]


