二次曲线族（具有某共同性质的二次曲线全体）
VLoG
次浏览
更新时间：2023-05-31
小编整理：
二次曲线族是由具有某种共同性质的二次曲线的全体组成的集合，可以简化求适合一定条件的二次曲线的方程的步骤。根据参数个数的不同，二次曲线族可以被分为单参数二次曲线族、双参数二次曲线族等。二次曲线族
具有某共同性质的二次曲线全体
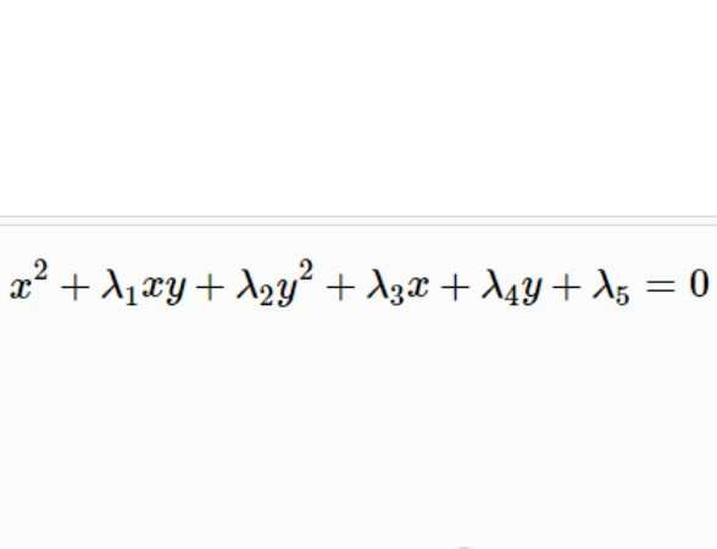
二次曲线族是二次曲线的集合，指具有某种共同性质的二次曲线的全体，它可简化求适合一定条件的二次曲线的方程的步骤，随着独立参数个数的不同，把二次曲线族按其参数的个数而分为单参数二次曲线族、双参数二次曲线族等。
基本信息
| 中文名 | 二次曲线族 |
| 所属问题 | 平面几何 |
| 简介 | 具有某共同性质的二次曲线全体 |
| 所属学科 | 数学 |
基本概念
在二次曲线的方程
如果二次方程(1)的参数满足
，那么这二次方程所含的独立参数的个数就由五个减到三个而成为三参数二次曲线族，即 圆族。
如果二次方程(1)的参数满足
,那么这二次方程所含的独立参数的个数就由五个减到四个而成为四参数二次曲线族，即 抛物线族。
如果二次方程(1)的参数满足
,那么这二次方程所含的独立参数的个数并没有减少，仍为五个独立参数，是五参数二次曲线族，即 中心二次曲线族。
二次曲线族可简化求适合一定条件的二次曲线的方程的步骤：
1.给定两条二次曲线
，
，经过这两条二次曲线的所有交点(一般有4个)的二次曲线族的方程为
，式中
是不同时为零的参数。
2.经过两条直线
与二次曲线
的交点的二次曲线族的方程为
，式中λ是参数。
3.经过4点
的二次曲线族的方程为
，式中λ是参数，
。
4.与已知两直线
分别相切于已知点
)的二次曲线族的方程为
，式中
，λ是参数，例如，已知
和AB边上的中线OC上一点P，
，则与两直线AC，BC分别相切于点A，B，且过点P的二次曲线为
，当
时，图形为抛物线；当
时，图形为椭圆；当
时，图形为双曲线。
5.与二次曲线相切于已知点
的二次曲线族的方程为
，式中λ，μ是参数，
。
定理
下面仅讨论单参数二次曲线族，又称为二次曲线系。
定理1 如果给定两条二次曲线
，那么含有一个参数λ的方程：
是表示经过这两条二次曲线的所有交点(一般有四个)的二次曲线族，为了避免将曲线
遗漏掉，也将这二次曲线族的方程写成
定理1的证明过程与直线系的定理证明相仿。
定理2 如果已知两直线
和一条二次曲线
，那么含有一个参数λ的方程
是表示经过两直线与二次曲线的交点的二次曲线族。
证明 因为直线
与二次曲线的交点坐标满足式(2),所以曲线(2)过它们的交点，又方程(2)的次数不大于二次，所以，它是单参数二次曲线族。
定理4 与已知直线分别相切于已知点
，
的二次曲线族的方程为
这里直线
的方程是
。
