双曲线（应用于数学解析几何的函数曲线）

VLoG
VLoG
次浏览
更新时间：2023-05-31

小编整理：

双曲线（hyperbola）是一种圆锥曲线，由一个不通过直圆锥面的顶点的平面去截取圆锥体的两个叶得到。双曲线也是平面到两个固定的点的距离差为常数的点的轨迹，这个常数就是双曲线的焦距。 在数学解析几何中，双曲线是由方程 x^2/a^2 - y^2/b^2 = 1 表示的函数曲线，其中 a 和 b 是常数，且 a>0。双曲线的焦点在 x 轴上，并且永远是左右两个分支相互对称。 双曲线在数学、物理学和工程学中有广泛应用。例如，在光学中，双曲线被用于设计折射望远镜和反射望远镜；在物理学中，双曲线被用于描述电磁波、光学和量子力学等领域的现象；在数学中，双曲线被用于研究圆锥曲线、函数和不等式等主题。

双曲线

应用于数学解析几何的函数曲线
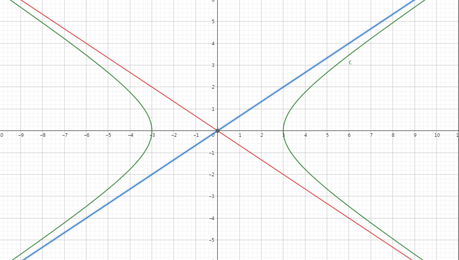
双曲线（英文：hyperbola）是常见的一类圆锥曲线，可以由一个不通过直圆锥面的顶点的平面去截取圆锥体的两个叶得到。双曲线也是平面到两个固定的点的距离差为常数的点的轨迹。
基本信息
中文名
双曲线
英文名
hyperbola
提出时间
16世纪
相关人物
梅内克谬斯、阿波罗尼奥斯、欧拉等
相关著作
《圆锥曲线论》 、《分析引论》
研究对象
解析几何
运用领域
数学

历史

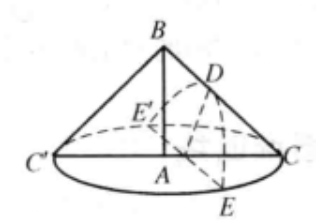
梅内克谬斯对双曲线的研究
约公元前 4 世纪，古希腊学者梅内克谬斯(Menaechmus)在研究平面与圆锥相交时最先发现了圆锥曲线，即椭圆，抛物线和双曲线是圆锥体表面与平面的交点产生的。如图所示，
为直角三角形，首先以
的短直角边 AB 为轴旋转一周得到圆锥体，然后取一垂直于斜边（BC边）的平面截取这个圆锥体切口形成的曲线即为双曲线。
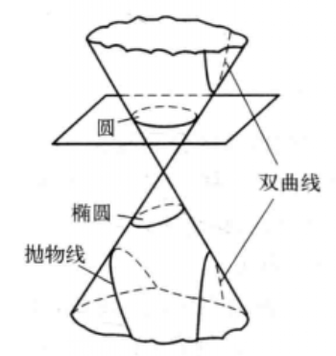
阿波罗尼奥斯对双曲线的研究
公元前2世纪，古希腊数学家阿波罗尼奥斯（Apollonius of Perga）从纯几何的思想出发，建立起系统的圆锥曲线理论。讨论如右图所示，他在同一个圆锥体中使用不同的切割面得到了圆、圆、双曲线、抛物线4种图形。阿波罗尼奥斯发表了数学著作《圆锥曲线论》，该著作详细介绍了双曲线等圆锥曲线的性质。
16世纪，德国数学家约翰内斯·开普勒（Johannes Kepler）发现了行星三大定律，意大利数学家伽利略·伽利雷（Galileo di Vincenzo Bonaulti de Galilei）基于运动合成的思想，发现了物体斜抛运动的轨迹为抛物线，人们开始意识到圆锥曲线不单是圆锥体的切割面，还与自然界的运动变化息息相关。
17世纪，法国数学家勒内·笛卡尔（René Descartes）和皮耶·德·费马（Pierre de Fermat）创立了解析几何，建立起坐标系的概念，用数学方程来研究圆锥曲线的各种性质。1745 年，瑞士数学家莱昂哈德·欧拉（Leonhard Euler）发表了《分析引论》，基于方程思想对圆锥曲线进行了系统的研究。

基本概念

定义

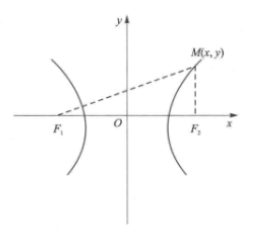
双曲线的定义
把平面内与两个定点
的距离差的绝对值等于常数 (小于
并且大于0) 的点的轨迹叫作双曲线，这两个定点称为双曲线的焦点，两焦点的距离叫作双曲线的焦距，焦距的一半长度称为半焦距。
如图所示，直角坐标系中
在
轴上，且线段
的中点与直角坐标系的原点相重合。设
为双曲线上任意一点，焦距为
，两焦点坐标为
。根据双曲线的定义，得方程
。
上述方程的曲线即为双曲线。

标准方程

对
整理可得：
。
上式记为式（1）。由于
，即
。
令
代人式得：
。
两边同除以
, 得：
。
该方程称为焦点在
轴上的双曲线的标准方程。式中,
满足关系式
。
如果双曲线的焦点在
轴上, 焦点为
。双曲线的标准方程为：
式中,
同样满足关系式
。

几何性质

焦点在
轴上的双曲线的标准方程
具有如下的几何性质，焦点在
轴上的双曲线的标准方程的性质可类似得出。

范围

整理方程
可以得到
。
也就是说
，即
或者
时，
才有意义。因此，双曲线不存在位于两条直线
和
之间的区域。

对称性

从双曲线的标准方程可以看到，双曲线的图像关于
轴、
轴和原点都是对称的，也就是说，两条坐标轴是双曲线的标准方程图像的对称轴，其中两个焦点所在的轴（
轴）称为焦点轴或实对称轴，另一条轴称为虚对称轴。此外，坐标原点为双曲线图像的对称中心点或者中心。

顶点

将
代入方程
可得，
。也就是说，双曲线与
轴存在两个交点，可记为
和
，这两个交点也称为双曲线的顶点，顶点相连的线段
称为双曲线的实轴，实轴的一半称为实半轴，长度为
。
将
代入方程
，解得
，可以看到
并没有实数解，也就是说，双曲线与
轴不能相交。如果在
轴上取两个点
，把线段
称为双曲线的虚轴，虚轴的一半称为虚半轴，长度为
。
从上述分析也可以看出，双曲线的焦点在实轴上，焦点和顶点总是在同一条对称轴。

渐近线

分别作两条对角线
，其斜率的绝对值为虚轴和实轴的长度之比，可以看到，双曲线图像局限在两条对角线之内，直线
称为双曲线的浙近线。 对于焦点在
轴上的双曲线
而言，其渐近线方䅣为
。
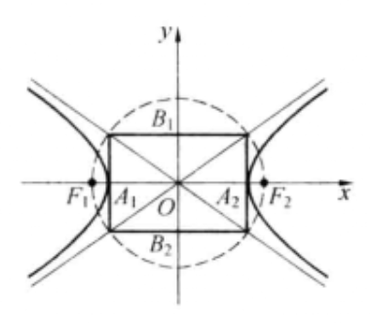
渐近线的做法
如图所示，可以根据如下步骤作出渐近线。
分别过
作出四条直线
和
，它们围成一个矩形。再画出该矩形的两条对角线，显然，这两条对角线为
，也就是该双曲线的浙近线。双曲线不与渐近线相交，但在离中心很远的地方，双曲线将无限接近于其渐近线。

离心率

定义双曲线的离心率
为焦距
与实轴
之比，即：
由于
，离心率
，离心率决定了双曲线的形状。离心率越大，双曲线的开口也就越大。若两条双曲线的离心率相等，那么这两条双曲线相似。

准线

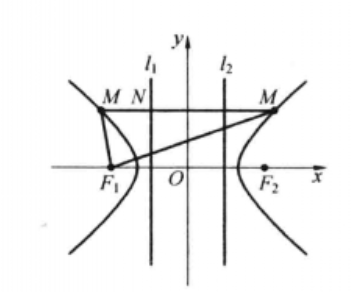
双曲线的准线
如图所示，直线
（即
）和直线
（即
）称为这条双曲线的准线，其中
叫作左准线，
叫作右准线。双曲线的准线具有以下的性质：
双曲线
上任意一点
到左焦点
的距离与它到左准线
的距离之比等于这双曲线的离心率
，任意一点
到右焦点
的距离与它到右准线
的距离之比也等于这双曲线的离心率
。

切线

对于双曲线的标准方程
或
来说，
曲线上的一点
对应的切线方程分别为：
或
若已知切线方程的斜率为
，则该切线方程分别为：
和
下表是双曲线两类标准的方程的部分性质。
标准方程
性 质
范 围
或
或
对称性
对称轴：坐标轴；对称中心:原点
顶 点
和
和
渐近线
离心率
，
实虚轴
线段
称为双曲线的实轴，实轴的一半称为实半轴，长度为
；线段
称为双曲线的虚轴，虚轴的一半称为虚半轴，长度为
满足关系式：
双曲线标准方程的几何性质，资料来源于：

表示方法

几何表示

如图所示，用一个不通过直圆锥面的顶点的平面去截取圆锥体的两个叶，所得的截痕是一条双曲线。该双曲线的焦点
为两个叶的内切球切点。

标准方程

当焦点位于
轴，即
，双曲线的标准方程为：
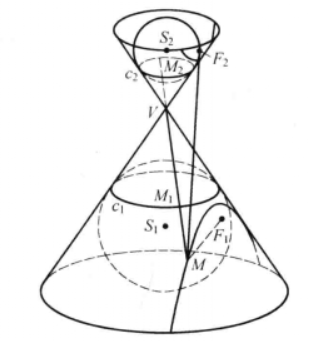
圆锥曲线的几何表示
上述方程也称为第一标准方程。
当焦点位于
轴，
，双曲线的标准方程为：
或
上述方程也称为第二标准方程。
在双曲线的标准方程中，
满足以下关系：

极坐标方程

建立如右图所示的极坐标，则双曲线的极坐标方程为：
式中，
与标准方程中的
存在如下关系：
,
。
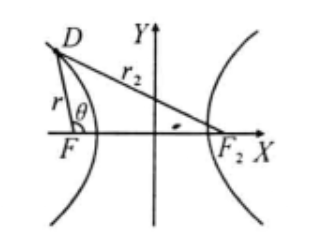
圆锥曲线的极坐标方程
当
，方程表示双曲线的右支，当
时，方程表示双曲线的左支。

参数方程

双曲线
的参数方程有如下多种表达形式。
类似地，双曲线
的参数方程也有以下对应的表达形式。

特殊的双曲线

等轴双曲线

实轴和虚轴相等的双曲线，称为等轴曲线，也称为直角双曲线。
由等轴双曲线的定义可知，以下曲线均为等轴双曲线。
所有等轴双曲线的离心率
，也就是说等轴双曲线都是相似的。此外，等轴双曲线的两条渐近线互相垂直。

共轭双曲线

如果一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴(这里的实轴和虚轴指的是线段)，则称这两条双曲线是共轭的。每条双曲线都叫作另一条双曲线的共轭双曲线。如果两条双曲线共轭，则这两条双曲线的四个焦点到共同中心是等距的，此外，它们有共同的渐近线。
由共轭双曲线的定义可知：
双曲线
和
互为共轭双曲线。

反比例函数

形如
的函数称为反比例函数。如右图所示，在平面直角坐标系中, 反比例函数
的图象是二次双曲线，
时, 该双曲线的两支分别位于一、三象限；
时, 该双曲线的两支分别位于二、四象限。
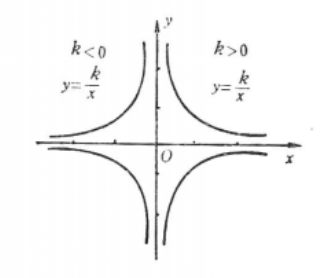
反比例函数的曲线是一种特殊的等轴双曲线，其图像关于原点对称，渐近线为
轴和
轴。反比例函数的图像可以看作把等轴双曲线的渐进线作为坐标轴后得到图像。
证明如下：
在直角坐标系
中，焦点位于
轴时，等轴双曲线的方程可以表示为：
等轴双曲线的两条渐近线互相垂直，因此可以将这两条渐近线旋转45°得到新的坐标系
，其坐标轴分别记为
轴。
该等轴双曲线上点在新的坐标系中的坐标与原坐标系坐标存在如下关系：
则新的坐标系中可以得到：
如果令
，
则有
。
不妨使用
代替
，
则有
，
即得到反比例函数的图像。

应用

双曲线是一种常见的二次曲线，在许多领域都有着广泛的用途。例如, 在军事上, 根据观察站所测得的炮声的时间差, 借助于双曲线方程, 就可以 确定出敌人的炮兵阵地的位置. 又如, 巴黎有名的埃菲尔铁塔是双曲线形的建筑。由双曲线生成 的曲面具有良好的抗压能力, 被广泛用于多类工程设计中, 能节省大量的建筑材料, 进而减少投资,降低成本。如许多水电站大坝就是采用的是双曲面构型。