柯西不等式(求解不等式的重要工具)

VLoG
次浏览
更新时间:2023-05-31
柯西不等式
求解不等式的重要工具
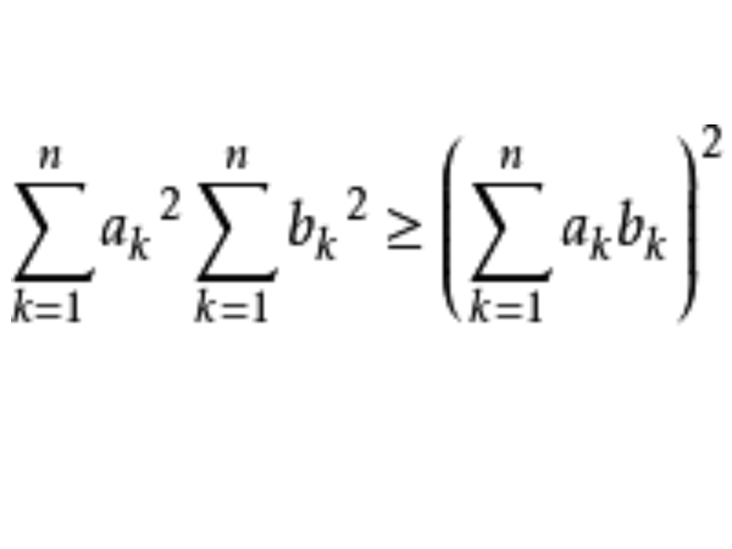
提出者简介
定义定理
向量形式


三角形式




概率论形式

积分形式

一般形式
设V是一线性空间,在V上定义了一个二元实函数,称为内积,记做 ,它具有以下性质:
,它具有以下性质:

1、

2、

3、

4、 ,当且仅当
,当且仅当 时
时



并定义α的长度 ,则柯西不等式表述为:
,则柯西不等式表述为:


验证推导
二维形式的证明




等号在且仅在 即
即 时成立。
时成立。


向量形式的证明

一般形式的证明
剩余几种情形都是一般情形的特例,完全可以用一般情形的证明方法来证。




定理推广
复变函数中的柯西不等式
若函数 在区域D及其边界上解析,
在区域D及其边界上解析, 内一点,以
内一点,以 为圆心做圆周
为圆心做圆周 ,只要
,只要 及其内部G均被D包含,则有:
及其内部G均被D包含,则有:






其中M是 的最大值。
的最大值。

证明:有柯西积分公式可知

所以




































