拉格朗日方程（拉格朗日力学的主要方程）

VLoG
VLoG
次浏览
更新时间：2023-07-18

小编整理：

拉格朗日方程是拉格朗日力学中的主要方程，用于描述物体的运动，特别是理论物理的研究。它与牛顿第二定律在牛顿力学中有着相似的功能，对于理解物理系统的运动和动力学性质具有重要意义。

拉格朗日方程

拉格朗日力学的主要方程
拉格朗日方程，因约瑟夫·路易斯·拉格朗日而命名，是拉格朗日力学的主要方程，可以用来描述物体的运动，特别适用于理论物理的研究。拉格朗日方程的功能相等于牛顿力学中的牛顿第二定律。
基本信息
中文名
拉格朗日方程
外文名
lagrange’s equations
别名
欧拉-拉格朗日方程
优势
广义坐标个数通常比x坐标少等

简介

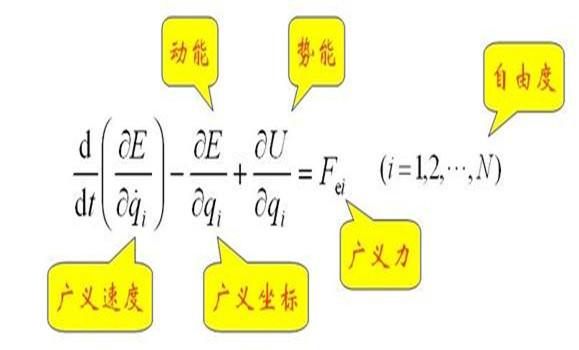
拉格朗日方程：对于完整系统用广义坐标表示的动力方程，通常系指第二类拉格朗日方程，是法国数学家J.-L.拉格朗日首先导出的。
通常可写成：
式中
为系统用各广义坐标
和各广义速度
所表示的动能；
为对应于
的广义力;
为这完整系统的自由度；
为系统的点数；
为完整约束方程个数。
从虚位移原理可以得到受理想约束的质点系不含约束力的平衡方程，而动静法(达朗贝尔原理)则将列写平衡方程的静力学方法应用于建立质点系的动力学方程，将这两者结合起来，便可得到不含约束力的质点系动力学方程，这就是动力学普遍方程。而拉格朗日方程则是动力学普遍方程在广义坐标下的具体表现形式。
通常，我们将牛顿定律及建立在此基础上的力学理论称为牛顿力学(也称矢量力学)，将拉格朗日方程及建立在此基础上的理论称为拉格朗日力学。拉格朗日力学通过位形空间描述力学系统的运动，它适合于研究受约束质点系的运动。拉格朗日力学在解决微幅振动问题和刚体动力学的一些问题的过程中起了重要的作用。拉格朗日方程可以用来建立不含约束力的动力学方程，也可以用来在给定系统运动规律的情况下求解作用在系统上的主动力。如果要想求约束力，可以将拉格朗日方程与动静法或动量定理(或质心运动定理)联用。

应用

用拉格朗日方程解题的优点是：①广义坐标个数通常比
坐标少，即
，故拉氏方程个数比直角坐标的牛顿方程个数少，即运动微分方程组的阶数较低，问题易于求解；②广义坐标可根据约束条件作适当的选择，使力学问题的运算简化，并且不必考虑约束力；③
和
都是标量，比力的矢量关系式更易表达，因此较易列出动力方程。下面是两个例子：
拉格朗日方程
①图1是一个半径为
、质量为
的圆盘，它的中心用铰链与质量为
的直杆相连。此杆的另一端用铰链固接在半径为
的空心圆筒的中心
；杆长
。圆盘绕
点摆动。杆的动能为
圆盘转动角关系为
，圆盘绕
点转动动能为
系统以
点为标准的势能
和系统的动能
为：
代入拉格朗日方程

形式

拉格朗日方程的一般形式是：式中
为用各广义坐标
和广义速度
导表示的系统的动能；
为对应
的广义力。方程式的个数等于系统的自由度N。保守系统中存在势函数
，则广义力距
，又因
中不含
，即
，故完整保守系统的拉格朗日方程为：
在非保守体系中，广义力不能用
表示，此时应引入广义势能
的概念，
.带入一般形式可以得到非保守体系的拉格朗日方程。
拉格朗日方程
式中
为拉格朗日函数，它等于系统的动势
与位势
之差。上式与变分问题中的欧拉方程形式相同，由此可导出哈密顿原理。