隧道效应（量子物理现象）

VLoG
VLoG
次浏览
更新时间：2023-05-20
隧道效应
本词条是多义词，共2个义项
量子物理现象
隧道效应由微观粒子波动性所确定的量子效应。又称势垒贯穿。考虑粒子运动遇到一个高于粒子能量的势垒，按照经典力学，粒子是不可能越过势垒的；按照量子力学可以解出除了在势垒处的反射外，还有透过势垒的波函数，这表明在势垒的另一边，粒子具有一定的概率，粒子贯穿势垒。
约瑟夫森效应属于遂穿效应，但有别于一般的隧道效应，它是库伯电子对通过由超导体间通过弱连接形成约瑟夫森结的超流效应。
基本信息
中文名
隧道效应
外文名
Tunnel effect
用途
定义
由
微观粒子
波动性确定的量子效应
又称
势垒贯穿
作用
理解许多
自然现象
的基础
收起
概念介绍
隧道效应
在势垒一边平动的粒子，当动能小于势垒高度时，按经典力学，粒子是不可能穿过势垒的。对于微观粒子，量子力学却证明它仍有一定的概率穿过势垒，实际也正是如此，这种现象称为隧道效应。对于谐振子，按经典力学，由核间距所决定的位能决不可能超过总能量。量子力学却证明这种核间距仍有一定的概率存在，此现象也是一种隧道效应。隧道效应是理解许多自然现象的基础。在两层金属导体之间夹一薄绝缘层，就构成一个电子的隧道结。实验发现电子可以通过隧道结，即电子可以穿过绝缘层，这便是隧道效应。使电子从金属中逸出需要逸出功，这说明金属中电子势能比空气或绝缘层中低．于是电子隧道结对电子的作用可用一个势垒来表示，为了简化运算，把势垒简化成一个一维方势垒。
隧道效应
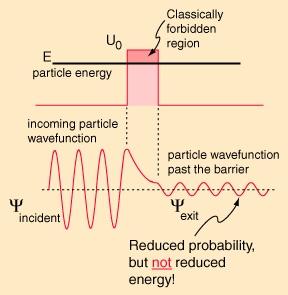
所谓隧道效应，是指在两片金属间夹有极薄的绝缘层（厚度大约为1nm（10-6mm），如氧化薄膜），当两端施加势能形成势垒V时，导体中有动能E的部分微粒子在E＜V的条件下，可以从绝缘层一侧通过势垒V而达到另一侧的物理现象。产生隧道效应的原因是电子的波动性。按照量子力学原理，有能量（动能）E的电子波长=（其中，——普朗克常数；——电子质量；E——电子的动能），在势垒V前：若E＞V，它进入势垒V区时，将波长改变为λ′=；若E＜V时，虽不能形成有一定波长的波动，但电子仍能进入V区的一定深度。当该势垒区很窄时，即使是动能E小于势垒V，也会有一部分电子穿透V区而自身动能E不变。换言之，在E＜V时，电子入射势垒就一定有反射电子波存在，但也有透射波存在。
效应原理
隧道效应
经典物理学人们认为，物体越过势垒，有一阈值能量；粒子能量小于此能量则不能越过，大于此能量则可以越过。例如骑自行车过小坡，先用力骑，如果坡很低，不蹬自行车也能靠惯性过去。如果坡很高，不蹬自行车，车到一半就停住，然后退回去。量子力学则认为，即使粒子能量小于阈值能量，很多粒子冲向势垒，一部分粒子反弹，还会有一些粒子能过去，好像有一个隧道，故名隧道效应（quantumtunneling）。可见，宏观上的确定性在微观上往往就具有不确定性。虽然在通常的情况下，隧道效应并不影响经典的宏观效应，因为隧穿几率极小，但在某些特定的条件下宏观的隧道效应也会出现。
发现者简介
隧道效应
1957年，受雇于索尼公司的江崎玲於奈（LeoEsaki，1940～）在改良高频晶体管2T7的过程中发现，当增加PN结两端的电压时电流反而减少，江崎玲於奈将这种反常的负电阻现象解释为隧道效应。此后，江崎利用这一效应制成了隧道二极管（也称江崎二极管）。1960年，美裔挪威籍科学家加埃沃（IvanGiaever，1929～）通过实验证明了在超导体隧道结中存在单电子隧道效应。在此之前的1956年出现的“库珀对”及BCS理论被公认为是对超导现象的完美解释，单电子隧道效应无疑是对超导理论的一个重要补充。1962年，年仅20岁的英国剑桥大学实验物理学研究生约瑟夫森（BrianDavidJosephson，1940～）预言，当两个超导体之间设置一个绝缘薄层构成SIS（Superconductor-Insulator-Superconductor）时，电子可以穿过绝缘体从一个超导体到达另一个超导体。约瑟夫森的这一预言不久就为P.W.安德森和J.M.罗厄耳的实验观测所证实——电子对通过两块超导金属间的薄绝缘层（厚度约为10埃）时发生了隧道效应，于是称之为“约瑟夫森效应”。宏观量子隧道效应确立了微电子器件进一步微型化的极限，在微电子器件进一步微型化时，必须要考虑上述的量子效应。举例来说，在制造半导体集成电路时，当电路的尺寸接近电子波长时，电子就通过隧道效应而穿透绝缘层，使器件无法正常工作。因此，宏观量子隧道效应已成为微电子学、光电子学中的重要理论。
主要用途
隧道效应本质上是量子跃迁，电子迅速穿越势垒。隧道效应有很多用途。如制成分辨力为0.1nm（1A）量级的扫描隧道显微镜，可以观察到Si的（111）面上的大元胞。但它适用于半导体样品的观察，不适于绝缘体样品的观测。在扫描隧道显微镜（STM）的启发下，1986年开发了原子力显微镜（AFM），其工作原理如图5所示。利用金刚石针尖制成以SiO2膜或Si3N4膜悬臂梁（其横向截面尺寸为100μm×1μm，弹性系数为0.1～1N/m），梁上有激光镜面反射镜。当针尖金刚石的原子与样品的表面原子间距离足够小时，原子间的相互作用力使悬臂梁在垂直表面方向上产生位移偏转，使入射激光的反射光束发生偏转，被光电位移传感器灵敏地探测出来。原子力显微镜对导体和绝缘体样品都适用，且其分辨力达到0.01mm（0.1A），可以测出原子间的微作用力，实现原子级表面观测。根据光隧道效应原理，利用光纤探测头、压电陶瓷、光电倍增管、扫描控制跟踪系统和微机，可以构成光隧道显微镜。它可以探测样品的表面形貌。在经典物理中，光在光纤内部全反射，在量子物理中，激光可以从一根光纤内通过隧道效应进入相距很近的另一个光纤内部，分光器就是利用量子隧道效应而制成的。放
隧道二极管
隧道效应
隧道二极管是一种具有负阻特性的半导体二极管。目前主要用掺杂浓度较高的锗或砷化镓制成。其电流和电压间的变化关系与一般半导体二极管不同。当某一个极上加正电压时，通过管的电流先将随电压的增加而很快变大，但在电压达到某一值后，忽而变小，小到一定值后又急剧变大；如果所加的电压与前相反，电流则随电压的增加而急剧变大。因为这种变化关系只能用量子力学中的“隧道效应”加以说明，故称隧道二极管。由于“江崎二极管”具有负电阻，并且隧道效应发生速度异常迅速，可用于高频振荡、放大以及开关等电路元件，尤其可以用来提高电子计算机的运算速度。
隧道巨磁电阻效应
隧道效应
超导隧道结的发现在理论和实验上均有重要的价值。受此启发Julliere对Fe/Ge/Co磁性隧道结输运性质的研究作了开拓性的研究，发现隧道阻抗随铁磁层的磁化状态而变化，低温下电导的相对变化可达14%。1975年后人们对类似结构中的磁电阻效应进行了研究，但在室温下均不能获得较大的磁电阻效应。在GMR效应全球研究浪潮推动下，1994年在“磁性金属/非磁绝缘体/磁性金属”（FM/I/FM）型隧道结Fe/Al2O3/Fe中获得了突破性进展。4.2K低温下，磁电阻变化率高达30%，室温下达18%。在这种结构中如果两铁磁层的磁化方向平行，一个铁磁层中多数自旋子带的电子将进入另一个电极中的多数自旋子带的空态，同时少数自旋子带的电子也从一电极进入另一电极的少数自旋子带的空态；如果两电极的磁化方向反平行，则一个电极中的多数子带的自旋与另一个电极的少数自旋子带电子的自旋平行，这样，隧道电导过程中一个电极中多数自旋子带的电子必须在另一个电极中寻找少数自旋子带的空态，因而其隧道电导必须与两极的磁化方向平行时的电导有所差别，将隧道电导与铁磁电极的磁化方向相关的现象称为磁隧道阀效应（magneticvalveeffect）。理论上假定电子穿越绝缘体势垒时保持其自旋方向不变，在实际制备过程中由于氧化层生成时难免导致相邻铁磁层氧化，致使反铁磁性的氧化薄层的出现影响磁电电阻效应。所以实验的结果比理论上的预计要小。Julliere模型给出磁隧道阀电阻的相对变化，即隧道磁电阻（TMR）RTM为。
隧道效应
式中：ρ1和ρ2分别是两个铁磁电极的自旋极化度。显然，ρ1，ρ2越大，则TMR也越高。因为Fe和Co的ρ值分别为40%和34%，故Julliere模型可得Fe/I/Co的24%，但Fe/Ge/Co的实验值与理论值有一定差距。在磁隧道阀中，磁场克服的铁磁层的矫顽力就可使它们的磁化方向转至磁场方向而趋于一致，这时TMR为极小值；若将磁场减小至负，矫顽力小的铁磁层的磁化方向首先反转，两铁磁层的磁化方向相反，隧道电阻为极大值。由于只需反转一个单纯的铁磁层，因而只需一个非常小的外场便可实现TMR极大值，所以其磁场灵敏度极高。Fe/Al2O3/Fe和CoFe/Al2O3的磁场灵敏度分别为8%/Oe和5%/Oe。这些结果是多层膜的GMR及氧化物的CMR远所难及的。另外，在磁隧道结中可以通过改变氧化层的厚度来改变零场下的电阻值，而磁隧道结电阻值并不因此而改变的。这在金属多层膜中是很难实现的。这样根据不同的器件的驱动电压不同可以设计出不同的磁隧道结。今后如能解决氧化层的稳定制备和制备过程中铁磁层的氧化问题，其工业应用前景非常可观。此外如果技术手段可以保证的话，制备多层氧化隧道结也许可以获得更为丰富的物理效应和应用价值。隧道结的磁电阻效应取得了突破之后，人们受颗粒膜的启发又在Ni-SiO2,Co-SiO2,Fe-MgF2以及Fe-SiO2的铁磁绝缘物颗粒膜中发现了高的磁电阻效应。实验表明该体系中磁电阻效应与磁性颗粒的大小有关，数值不大，饱和场较高，应用的前景可能不大。
宏观量子
隧道效应
各种元素的原子具有特定的光谱线，如钠原子具有黄色的光谱线。原子模型与量子力学已用能级的概念进行了合理的解释，由无数的原子构成固体时，单独原子的能级就并合成能带，由于电子数目很多，能带中能级的间距很小，因此可以看作是连续的，从能带理论出发成功地解释了大块金属、半导体、绝缘体之间的联系与区别，对介于原子、分子与大块固体之间的超微颗粒而言，大块材料中连续的能带将分裂为分立的能级；能级间的间距随颗粒尺寸减小而增大。当热能、电场能或者磁场能比平均的能级间距还小时，就会呈现一系列与宏观物体截然不同的反常特性，称之为量子尺寸效应。例如，导电的金属在超微颗粒时可以变成绝缘体，磁矩的大小和颗粒中电子是奇数还是偶数有关，比热亦会反常变化，光谱线会产生向短波长方向的移动，这就是量子尺寸效应的宏观表现。因此，对超微颗粒在低温条件下必须考虑量子效应，原有宏观规律已不再成立。
电子具有粒子性又具有波动性，因此存在隧道效应。近年来，人们发现一些宏观物理量，如微颗粒的磁化强度、量子相干器件中的磁通量等亦显示出隧道效应，称之为宏观的量子隧道效应。量子尺寸效应、宏观量子隧道效应将会是未来微电子、光电子器件的基础，或者它确立了现存微电子器件进一步微型化的极限，当微电子器件进一步微型化时必须要考虑上述的量子效应。例如，在制造半导体集成电路时，当电路的尺寸接近电子波长时，电子就通过隧道效应而溢出器件，使器件无法正常工作，经典电路的极限尺寸大概在0．25微米。目前研制的量子共振隧穿晶体管就是利用量子效应制成的新一代器件。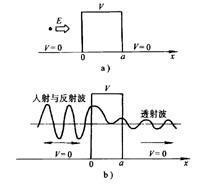
隧道视野效应
隧道效应
美国的一个摄制组，想拍一部中国农民生活的记录片。于是他们来到中国某地农村，找到一位柿农，说要买他1000个柿子，请他把这些柿子从树上摘下来，并演示一下贮存的过程，谈好的价钱是1000个柿子给20美元。柿农很高兴地同意了。于是他找来一个帮手，一人爬到柿子树上，用绑有弯钩的长杆，看准长得好的柿子用劲一拧，柿子就掉了下来。下面的一个人就从草丛里把柿子找了出来，捡到一个竹筐里。柿子不断地掉下来，滚得到处都是。下面的人则手脚飞快地把它们不断地捡到竹筐里，同时还不忘高声大嗓地和树上的人拉着家常。在一边的美国人觉得这很有趣，自然全都拍了下来。接着又拍了他们贮存柿子的过程。
美国人付了钱就准备离开，那位收了钱的柿农却一把拉住他们说："你们怎么不把买的柿子带走呢？"美国人说不好带，也不需要带，他们买这些柿子的目的已经达到了，这些柿子还是请他自己留着。"天底下哪有这样便宜的事情呢？"那位柿农心里想。看着美国人远去的背影，柿农摇摇头感叹道："没想到世界上还有这样的傻瓜！"那位柿农不知道，他的1000个柿子虽然原地没动地就卖了20美元，但那几位美国人拍的他们采摘和贮存柿子的记录片，拿到美国去却可以卖更多更多的钱。他也不知道，在那几个美国人眼里，他的那些柿子并不值钱，值钱的是他们的那种独特有趣的采摘、贮存柿子的生产生活方式。柿农的蝇头小利比起那几个美国人的利益来说实在不算什么。在企业的投资构成中，人们的决策者是像文中的柿农一样只看到眼前的比较直接的"小利益"还是能把眼光放长远一些，发现更大，但可能比较隐蔽的"大利益"呢？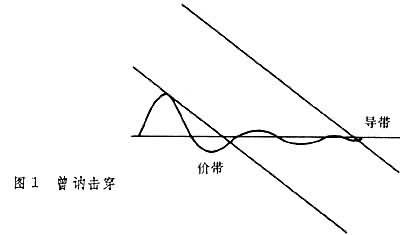
半导体
隧道效应
隧道效应──微观粒子能透入按经典力学规律它不可能进入的势垒区，是反映微观粒子的波动性的一种基本效应。可以把半导体（或绝缘体）中的电子迁移现象理解为在外电场下，束缚在一个原子中的电子，通过隧道穿透势垒，到另一个原子中。不过，通常说的半导体中的隧道效应指的不是这种对原子势场的量子隧道效应。而是指电子对半导体中宏观势垒的穿透，这个宏观势垒是半导体的禁带造成的。C.曾讷在1934年最先提出，在外电场下，固体的能带在空间上变成图1[曾讷击穿]所示的倾斜情况，价带的电子可以穿过禁带进入导带。在禁带中电子波函数指数衰减（波矢是复数的），就和穿过势垒时相似；曾讷认为这是强场下半导体(或绝缘体)电击穿的一种原因。但实验表明，通常半导体电击穿过程中，这种原因（称曾讷击穿）只起很次要的作用。只有在某些特殊类型的PN结的反向击穿中，才有以曾讷击穿为主的情况。这种类型的PN结称曾讷二极管，或按其用途叫稳压二极管。通常是硅二极管。
隧道效应
1957年江崎玲於奈发明了隧道二极管。它是高掺杂半导体形成的窄的PN结；当它加上前向偏压时,N区电子可以通过隧道效应，穿过禁带进入P区中价带的空状态。随所加的偏压增大，开始时隧道电流变大（可以进入的空状态增多）；随后到达极大值然后逐渐下降（可以进入的空状态减少），最后下降到零（可以进入的空状态没有了）。图2[隧道二极管伏安特性曲线]是隧道二极管的伏安特性曲线，以及对应各部分的PN结能带图。隧道二极管正向伏安特性中有一段负阻区，而且它还是一种多数载流子效应，没有渡越时间的限制，所以隧道二极管可用作低噪声的放大器、振荡器或高速开关器件，频率可达毫米波段。它作为器件的缺点是功率容量太小。隧道过程中，常常有电子－声子相互作用或电子-杂质相互作用参加。从隧道二极管的伏安特性上可分析出参与隧道过程的某些声子的频率。在势垒区中的光吸收或发射中，隧道效应也起着作用，这称夫兰克－凯尔德什效应。杂质的束缚电子态和能带中电子态之间的隧道也观察到。
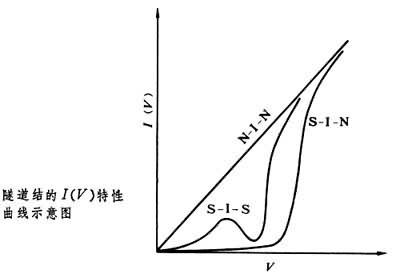
江崎玲於奈的发明开创了研究固体中隧道效应的新阶段。因此，他和发现超导体中隧道现象的I.加埃沃、B.D.约瑟夫森一起获得了1973年诺贝尔物理学奖。金属半导体接触势垒（肖脱基势垒）中的隧道现象也很有趣。1932年,A.H.威耳孙、.约飞'"class=link>..约飞和..夫伦克耳企图用隧道电流来解释肖脱基势垒的整流效应，但发现所预言的整流方向是错误的。不过，近年来却发现有些高掺杂的肖脱基势垒在小的前向偏压下，隧道电流是主要的电流机制。金属－绝缘体－半导体系统中隧道效应的研究也是有意义的。
相关词条
柳文扬，空间折叠，梦枕獏，宇宙弦，相空间，IFO，51区。