点阵(反映晶体结构周期性引入的概念)

VLoG
次浏览
更新时间:2023-05-20
简介
点阵
学说
19世纪出现了布喇菲(A.Bravais)的空间点阵学说,这一学说能解释有理指数定律和晶面角守恒定律,但它只是合理的猜想,其正确性到1912年才被劳厄(Laue,MaxTheodorFelixyon)等人的x射线衍射实验证实。几十年来的研究已探明了成千上万的晶体结构,肯定了晶体的周期性。
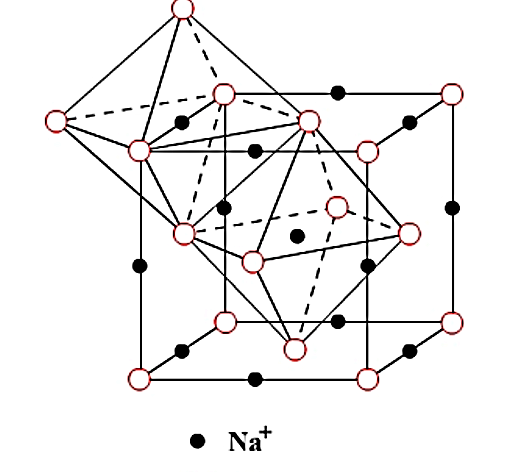
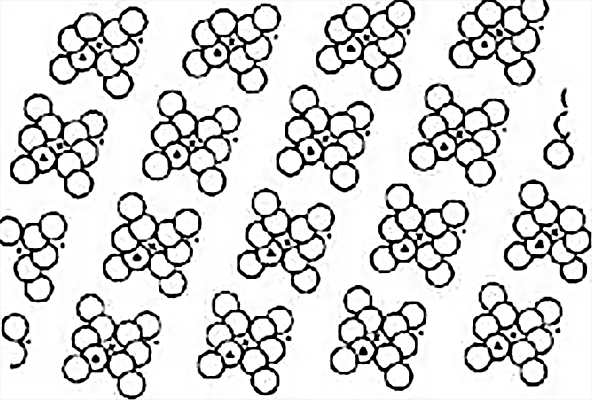
晶体中原子或原子团在三维空间有规律的周期排列构成了晶体结构。为了研究方便,人们忽略了那些种类繁多的原子和原子团,而把晶体看成是一些几何点在空间有规律的周期排列,同时,这些点与实际晶体中的原子又具有某种固定的空间位置关系。
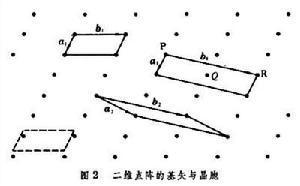
设想在空间有一组平行的等距离平面,与另外一组等距离平面相交,然后,它们又与第三组等距离的平行平面相交。结果,两两面相交的交线便构成了空间分布的格子,而交线的相交点便是空间分布的点,这些空间周期分布的点构成空间点阵。其中每个阵点的周围环境都相同,这就是说,每个阵点周围的阵点数以及各阵点相对参考点的取向相同。
点阵中的平行六面体称为阵胞。实际上,有许多种方式取平行六面体作为阵胞。描述阵胞的形状和大小采用3个矢量,即若以阵胞某角点为原点,沿3个棱边作3个矢量;通常面对的为a,向右为b,向上为c。它们之间的夹角分别为α,β和γ,称a、b、c和α,β和γ为阵胞的点阵参数。阵胞是点阵的基本单元,借阵胞的无限平移可以得到整个点阵。
表示方法
选取方式
晶体学
由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:
①要能充分反映整个空间点阵的周期性和对称性;
②在满足①的基础上,单胞要具有尽可能多的直角;
③在满足①、②的基础上,所选取单胞的体积要最小。
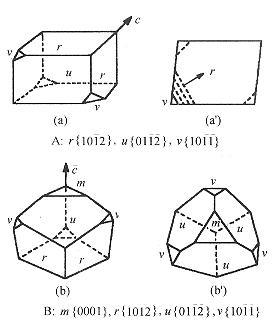
根据以上原则,所选出的14种布拉菲点阵的单胞可以分为两大类。一类为简单单胞,即只在平行六面体的8个顶点上有结点,而每个顶点处的结点又分属于8个相邻单胞,故一个简单单胞只含有一个结点。另一类为复合单胞(或称复杂单胞),除在平行六面体顶点位置含有结点之外,尚在体心、面心、底心等位置上存在结点,整个单胞含有一个以上的结点。14种布拉菲点阵中包括7个简单单胞,7个复合单胞。
具体内容
点阵
简单点阵:a、b、c;
底心点阵:a、b、c、(a+b)/2;
体心点阵:a、b、c、(a+b+c)/2;
面心点阵:a、b、c、(a+b)/2、(b+c)/2、(a+c)/2;
所以布拉菲点阵也称为平移点阵。
点阵字体
定义
点阵字体是把每一个字符都分成16×16或24×24个点,然后用每个点的虚实来表示字符的轮廓。点阵字体优点是显示速度快,不像矢量字体需要计算;其最大的缺点是不能放大,一旦放大后就会发现文字边缘的锯齿。
表现形式

点阵
矢量字库

点阵