正比例函数(一次函数的一种特殊形式)

VLoG
次浏览
更新时间:2023-05-22
正比例函数
一次函数的一种特殊形式
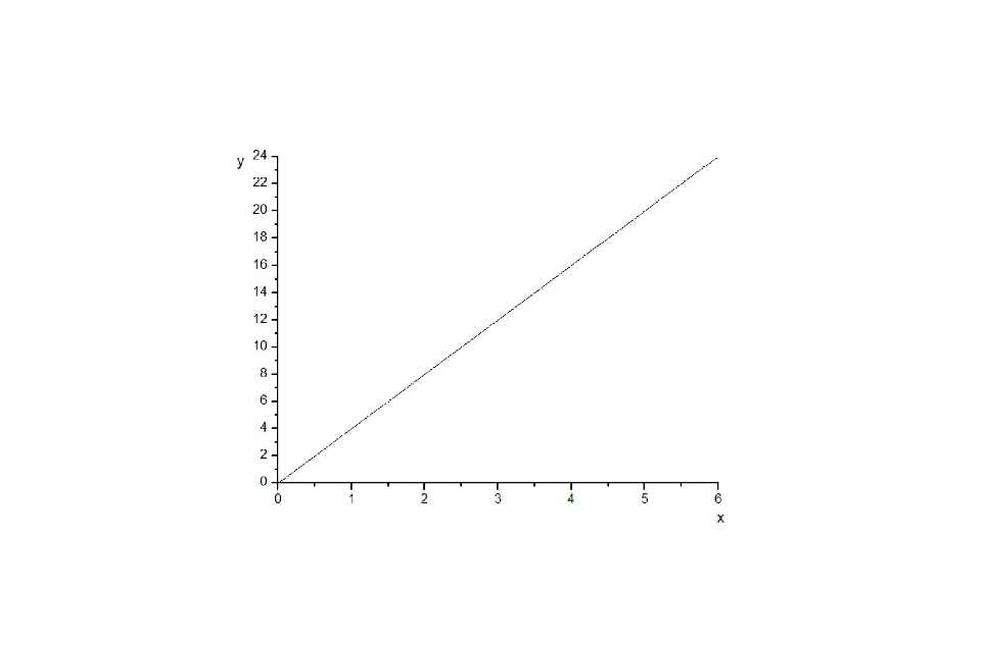
基本信息
| 中文名 | 正比例函数 |
| 外文名 | directly proportional function |
| 提出者 | Jack louny |
| 表达式 | y=kx |
| 应用学科 | 数学 |
展开
定义
正比例函数属于一次函数,是一次函数的一种特殊形式。即一次函数形如: (k为常数,且k≠0)中,当b=0时,则叫做正比例函数。一般地,形如
(k为常数,且k≠0)中,当b=0时,则叫做正比例函数。一般地,形如 (k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线
(k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线 。
。



性质
图像
图像作法
(一)
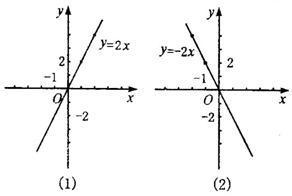
正比例函数的图片
2、根据第一步求的x、y的值描出点;
3、作出第二步描出的点和原点的直线(因为两点确定一直线)。
(二)
1、已知一点坐标,用待定系数法求函数解析式。先设解析式为 ,再代入已知点坐标,解出k的值;
,再代入已知点坐标,解出k的值;

2、解出k的值后,在数轴上标出各点并连接个点。
正比例

③正比例关系两种相关联的量的变化规律:对于比值为正数的,即y=kx(K为常数,k≠0),此时的y与x,同时扩大,同时缩小,比值不变。例如:汽车每小时行驶的速度一定,所行的路程和所用的时间 成正比例。以上各种商都是一定的,那么被除数和除数所表示的两种相关联的量成正比例关系。
注意:在判断两种相关联的量是否成正比例时,应注意这两种相关联的量,虽然也是一种量随着另一种的变化而变化,但它们相对应的两个数的比值不一定,那它们就不能成正比例。例如:一个人的年龄和它的体重,就不能成正比例关系,正方形的边长和它的面积也不成正比例关系。而单价数量与总价是成正比的(单价不变,总价随着数量的增减而增减)。
例题
相关视频
全部
3973次播放03:56
数学大师:正比例函数
简介
1万次播放02:34
【一次函数】 03 正比例函数的概念
定义
9774次播放03:00
【一次函数】 04 正比例函数的图象与性质
单调性







